Evolutionary graph theory
Evolutionary dynamics act on populations. Neither genes, nor cells, nor individuals but populations evolve. In small populations, random drift dominates, whereas large populations are sensitive to subtle differences in selective values. Traditionally, evolutionary dynamics was studied in the context of well-mixed or spatially extended populations. Here we generalize population structure by arranging individuals on a graph. Each vertex represents an individual. The fitness of an individual denotes its reproductive rate, which determines how often offspring is placed into adjacent vertices.
Popular population structures include well-mixed (or 'unstructured') populations, which correspond to fully connected (or complete) graphs or populations with spatial dimensions that are represented by lattices. Other, more general population structures include small-world or scale-free networks.
The dynamics of selection and random drift in finite populations is traditionally modelled by the Moran process. This process has the nice feature that the population size is preserved.
In the following, we study the simplest possible question: what is the probability that a single mutant generates a lineage that takes over the entire population? This fixation probability determines the rate of evolution. The higher the correlation between the mutant's fitness and its probability of fixation, the stronger the effect of natural selection; if fixation is largely independent of fitness, drift dominates.
A large class of graphs exhibit a characteristic balance between selection and drift as characterised by the circulation theorem. Nevertheless, the structure of the graphs can have tremenduous effects on the fixation probability of mutant ranging from complete suppression of selection to complete suppression of random drift, i.e. amplification of selection. If, in addition, individuals interact with their neighbors, reflecting frequency dependent fitness, the dynamics becomes very complicated but first studies show very interesting and counterintuitive results.
Moran graphs
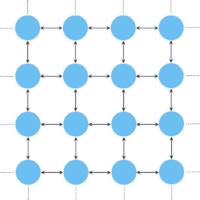
Population structure can be introduced by assuming that the individuals occupy the nodes of a graph. The adjacency matrix \(W = [w_{ij}]\) then determines the structure of the graph, where \(w_{ij}\) denotes the probability that individual \(i\) places its offspring into node \(j\). If \(w_{ij} = w_{ji} = 0\) then the nodes \(i\) and \(j\) are not connected. Interestingly, the fixation probability remains unaffected for a large class of population structures (graphs known as circulations), i.e. is the same as for the original Moran process in unstructured populations: \[ \rho_1 = \frac{\displaystyle 1-\frac1r}{\displaystyle 1-\frac1{r^N}}. \] This holds, for example, for the fixation probabilities of mutants on lattices.
Evolutionary suppressors

The characteristic balance between selection and drift in Moran graphs can tilt to either side for graphs that are not circulations. For example, suppose \(N\) individuals are arranged in a linear chain. Each individual places its offspring into the position immediately to its right. The leftmost individual is never replaced. The mutant can only reach fixation if it arises in the leftmost position, which happens with probability \(1/N\), but then it will eventually reach fixation with certainty. Clearly, for such one-rooted graphs the fixation probability of a randomly placed mutant is \[ \rho_0 = \frac1N, \] irrespective of \(r\). The chain is an example of a simple population structure which eliminates selection and whose dynamic is determined by random drift.
Evolutionary amplifiers
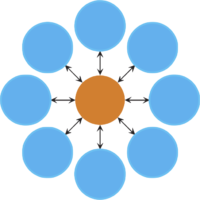
Interestingly, it is also possible to create population structures that amplify selection and suppress random drift. For example, on the star structure, where all nodes are connected to a central hub and vice versa, the fixation probability of a randomly placed mutant becomes \[ \rho_2 = \frac{\displaystyle 1-\frac1{r^2}}{\displaystyle 1-\frac1{r^{2N}}}. \] for large \(N\). Thus, any selective difference \(r\) is amplified to \(r^2\). Even more intriguingly, population structures exist that act as arbitrarily strong amplifiers of selection and suppressors of random drift. However, note that amplification has its price in that the average fixation time goes to infinity as the amplification increases.
Moran process
The Moran process describes the stochastic evolution in a finite, unstructured (well-mixed) population of constant size \(N\), which is composed of residents (white) and mutants (black):

Setup: The state of the population is given by the number of residents and mutants.

Step 1: At each time step a focal individual is chosen for reproduction with a probability proportional to its fitness (here, resident is selected for reproduction).
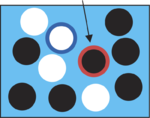
Step 2: A randomly chosen individual is eliminated (here, mutant is selected for death).

Step 3: The offspring replaces the eliminated individual.
This process is repeated until either one of the two absorbing states is reached: a homogeneous state of either all residents (mutant went extinct) or all mutants (resident displaced). No other stable equilibrium state is possible. Whenever an absorbing state is reached, mutants (residents) are said to have reached fixation. The corresponding fixation probability and fixation time are important markers to characterize the evolutionary process. The Moran process represents a specific balance between selection and drift: advantageous mutations have a certain chance - but no guarantee - of fixation, whereas disadvantageous mutants are likely - but again, no guarantee - to become extinct.
Spatial Moran process
The Moran process can be easily generalized to structured populations or graphs by restricting step 2 above such that the offspring of the focal individual replaces one of its neighbours rather than a random member of the population.
Publications
- Lieberman, E., Hauert, C. & Nowak, M. (2005) Evolutionary dynamics on graphs Nature 433 312-316 doi: 10.1038/nature03204.
- Jamieson-Lane, A. & Hauert, C. (2015) Fixation probabilities on superstars, revisited and revised J. Theor. Biol. 382 44-56 doi: 10.1016/j.jtbi.2015.06.029.
Press & News
- Guimerà, R. & Sales-Pardo, M. (2006) Form follows function: the architecture of complex networks Molecular Systems Biology 2 42 doi: 10.1038/msb4100082.
References
- Moran, P. A. P. (1962) Random processes in genetics Proc. Cambridge Phil. Soc. 54 60-71.
- Maruyama, T. (1974) A Simple Proof that Certain Quantities are Independent of the Geographical Structure of Population Theor. Pop. Biol. 5 148-154.
- Slatkin, M. (1981) Fixation probabilities and fixation times in a subdivided population Evolution 35 477-488.
