Tutorials: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
== [[Stochastic dynamics in finite populations]] == | == [[Stochastic dynamics in finite populations]] == | ||
[[Image:RSP - SDE.svg|160px|left|link=Stochastic dynamics in finite populations]] | {| | ||
Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations. | | style="vertical-align:top" |[[Image:RSP - SDE.svg|160px|left|link=Stochastic dynamics in finite populations]] | ||
| style="vertical-align:top" |Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations. | |||
<div class="footnote" style=" | <div class="footnote" style="font-size:smaller"> | ||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2012) ''Phys. Rev. E'' | #Traulsen, A., Claussen, J. C. & Hauert, C. (2012) ''Phys. Rev. E'' '''85''' 041901 [http://dx.doi.org/10.1103/PhysRevE.85.041901 doi: 10.1103/PhysRevE.85.041901]. | ||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2006) ''Phys. Rev. E'' '''74''' 011901 [http://dx.doi.org/10.1103/PhysRevE.74.011901 doi: 10.1103/PhysRevE.74.011901]. | #Traulsen, A., Claussen, J. C. & Hauert, C. (2006) ''Phys. Rev. E'' '''74''' 011901 [http://dx.doi.org/10.1103/PhysRevE.74.011901 doi: 10.1103/PhysRevE.74.011901]. | ||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2005) ''Phys. Rev. Lett.'' '''95''' 238701 [http://dx.doi.org/10.1103/PhysRevLett.95.238701 doi: 10.1103/PhysRevLett.95.238701]. | #Traulsen, A., Claussen, J. C. & Hauert, C. (2005) ''Phys. Rev. Lett.'' '''95''' 238701 [http://dx.doi.org/10.1103/PhysRevLett.95.238701 doi: 10.1103/PhysRevLett.95.238701]. | ||
</div> | </div> | ||
|} | |||
{{-}} | {{-}} | ||
== [[Evolutionary Games and Population Dynamics]] == | == [[Evolutionary Games and Population Dynamics]] == | ||
[[Image:Evolutionary games and population dynamics.gif|left|160x160px|link=Evolutionary Games and Population Dynamics]] | {| | ||
Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups. | | style="vertical-align:top" | [[Image:Evolutionary games and population dynamics.gif|left|160x160px|link=Evolutionary Games and Population Dynamics]] | ||
| style="vertical-align:top" |Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups. | |||
<div class="footnote" style=" | <div class="footnote" style="font-size:smaller"> | ||
# Wakano, J. Y. & Hauert, Ch. (2011) J. theor. Biol. 268 30-38 [http://dx.doi.org/10.1016/j.jtbi.2010.09.036 doi: 10.1016/j.jtbi.2010.09.036]. | # Wakano, J. Y. & Hauert, Ch. (2011) J. theor. Biol. 268 30-38 [http://dx.doi.org/10.1016/j.jtbi.2010.09.036 doi: 10.1016/j.jtbi.2010.09.036]. | ||
# Wakano, J. Y., Nowak, M. A. & Hauert, Ch. (2009) Proc. Natl. Acad. Sci. USA 106 7910-7914 [http://dx.doi.org/10.1073/pnas.0812644106 doi: 10.1073/pnas.0812644106]. | # Wakano, J. Y., Nowak, M. A. & Hauert, Ch. (2009) Proc. Natl. Acad. Sci. USA 106 7910-7914 [http://dx.doi.org/10.1073/pnas.0812644106 doi: 10.1073/pnas.0812644106]. | ||
| Line 23: | Line 26: | ||
# Hauert, C., Holmes, M. & Doebeli, M. (2006) Proc. R. Soc. Lond. B '''273''', 2565-2570 [http://dx.doi.org/10.1098/rspb.2006.3600 doi: 10.1098/rspb.2006.3600]. | # Hauert, C., Holmes, M. & Doebeli, M. (2006) Proc. R. Soc. Lond. B '''273''', 2565-2570 [http://dx.doi.org/10.1098/rspb.2006.3600 doi: 10.1098/rspb.2006.3600]. | ||
</div> | </div> | ||
|} | |||
{{-}} | {{-}} | ||
== [[Origin of Cooperators and Defectors]] == | == [[Origin of Cooperators and Defectors]] == | ||
[[Image:Origin of cooperators and defectors.gif|left|160x160px|link=Origin of Cooperators and Defectors]] | {| | ||
Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial. | | style="vertical-align:top" |[[Image:Origin of cooperators and defectors.gif|left|160x160px|link=Origin of Cooperators and Defectors]] | ||
| style="vertical-align:top" |Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial. | |||
<div class="footnote" style=" | <div class="footnote" style="font-size:smaller"> | ||
# Killingback, T., Doebeli, M. & Hauert, Ch. (2010) Biological Theory 5, 3-6 [http://dx.doi.org/10.1162/BIOT_a_00019 doi: 10.1162/BIOT_a_00019]. | # Killingback, T., Doebeli, M. & Hauert, Ch. (2010) Biological Theory 5, 3-6 [http://dx.doi.org/10.1162/BIOT_a_00019 doi: 10.1162/BIOT_a_00019]. | ||
# Doebeli, M., Hauert, C. & Killingback, T. (2004) Science '''306''', 859-862 [http://dx.doi.org/10.1126/science.1101456 doi: 10.1126/science.1101456]. | # Doebeli, M., Hauert, C. & Killingback, T. (2004) Science '''306''', 859-862 [http://dx.doi.org/10.1126/science.1101456 doi: 10.1126/science.1101456]. | ||
</div> | </div> | ||
|} | |||
{{-}} | {{-}} | ||
== [[2×2 Games]] == | == [[2×2 Games]] == | ||
[[Image:Cover IJBC 2002.12.png| | {| | ||
Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world. | | style="width:160px; text-align:center; vertical-align:top" | [[Image:Cover IJBC 2002.12.png|center|160x160px|link=2×2 Games]] | ||
| style="vertical-align:top" | Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world. | |||
<div class="footnote" style=" | <div class="footnote" style="font-size:smaller"> | ||
# Hauert, C. (2002) Int. J. of Bifurcation & Chaos '''12''' 1531-1548 [http://dx.doi.org/10.1142/S0218127402005273 doi: 10.1142/S0218127402005273]. | # Hauert, C. (2002) Int. J. of Bifurcation & Chaos '''12''' 1531-1548 [http://dx.doi.org/10.1142/S0218127402005273 doi: 10.1142/S0218127402005273]. | ||
# Hauert, C. (2001) Proc. R. Soc. Lond. B 268, 761-769 [http://dx.doi.org/10.1098/rspb.2000.1424 doi: 10.1098/rspb.2000.1424]. | # Hauert, C. (2001) Proc. R. Soc. Lond. B 268, 761-769 [http://dx.doi.org/10.1098/rspb.2000.1424 doi: 10.1098/rspb.2000.1424]. | ||
</div> | </div> | ||
|} | |||
{{-}} | {{-}} | ||
Revision as of 17:22, 3 May 2012
Stochastic dynamics in finite populations
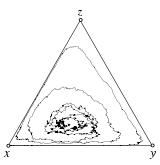 |
Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations.
|
Evolutionary Games and Population Dynamics
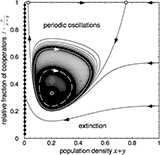 |
Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups.
|
Origin of Cooperators and Defectors
 |
Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial.
|
2×2 Games
 |
Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world.
|
