Tutorials: Difference between revisions
No edit summary |
|||
| Line 4: | Line 4: | ||
{| | {| | ||
| style="vertical-align:top" |[[Image:Superstar graph (N=484, B=21, k=6).svg|160px|left|link=Evolutionary graph theory]] | | style="vertical-align:top" |[[Image:Superstar graph (N=484, B=21, k=6).svg|160px|left|link=Evolutionary graph theory]] | ||
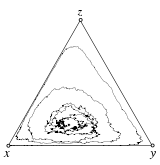
| style="vertical-align:top" |Tutorial on evolutionary graph theory, which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in | | style="vertical-align:top" |Tutorial on [[evolutionary graph theory]], which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in structured populations. Interestingly, the fixation probabilities remain unaffected by the underlying structure for a [[Moran graphs|large class of graphs]]. However, some graphs may act either as [[Evolutionary amplifiers|amplifiers]] or [[Evolutionary suppressors|suppressors]] of selection by increasing or decreasing the fixation probabilities as compared to unstructured populations. In contrast, fixation and absorption times are very sensitive to changes in the graph structure and hence vary greatly even for graphs that leave fixation probabilities unchanged. Even though fixation times are, in general, not preserved between graphs, [[Graph symmetries|symmetries of a graph]] can at least ensure that fixation times do not depend on the initial location of the mutant. This summarizes research efforts that span over a decade, including: | ||
<div class="footnote" style="font-size:smaller"> | <div class="footnote" style="font-size:smaller"> | ||
#Lieberman, E., Hauert, C. & Nowak, M. (2005) ''Nature'' '''433''' 312-316 [http://dx.doi.org/10.1038/nature03204 doi: 10.1038/nature03204]. | #Lieberman, E., Hauert, C. & Nowak, M. (2005) ''Nature'' '''433''' 312-316 [http://dx.doi.org/10.1038/nature03204 doi: 10.1038/nature03204]. | ||
Latest revision as of 10:52, 31 August 2016
Evolutionary graph theory
 |
Tutorial on evolutionary graph theory, which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in structured populations. Interestingly, the fixation probabilities remain unaffected by the underlying structure for a large class of graphs. However, some graphs may act either as amplifiers or suppressors of selection by increasing or decreasing the fixation probabilities as compared to unstructured populations. In contrast, fixation and absorption times are very sensitive to changes in the graph structure and hence vary greatly even for graphs that leave fixation probabilities unchanged. Even though fixation times are, in general, not preserved between graphs, symmetries of a graph can at least ensure that fixation times do not depend on the initial location of the mutant. This summarizes research efforts that span over a decade, including:
|
Stochastic dynamics in finite populations
 |
Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations.
|
Evolutionary Games and Population Dynamics
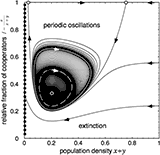 |
Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups.
|
Origin of Cooperators and Defectors
 |
Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial.
|
2×2 Games
 |
Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world.
|
