EvoLudo: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div id="mainpage_topbox"> | <div id="mainpage_topbox">__NOTOC__ | ||
<div id="mainpage_pagetitle">'''Welcome to ''EvoLudo'' | <div id="mainpage_pagetitle">'''Welcome to ''EvoLudo'''''</div> | ||
''EvoLudo'' is a growing collection of interactive tutorials that complement numerous research articles on evolutionary games ([https://en.wiktionary.org/wiki/ludo ''ludo''] Latin for "I play" or Italian for "game"). These tutorials allow the reproduction and verification of results reported in [[Research|scientific articles]]. In addition, they are intended to encourage the interested reader, students and researchers to explore the fascinating world of game theory and evolutionary dynamics in a playful manner. This helps to develop a better intuitive understanding of the often complex evolutionary dynamics and encourage further explorations in the fascinating and often mesmerizing world of spatio-temporal patterns. | ''EvoLudo'' is a growing collection of interactive tutorials that complement numerous research articles on evolutionary games ([https://en.wiktionary.org/wiki/ludo ''ludo''] Latin for "I play" or Italian for "game"). These tutorials allow the reproduction and verification of results reported in [[Research|scientific articles]]. In addition, they are intended to encourage the interested reader, students and researchers to explore the fascinating world of game theory and evolutionary dynamics in a playful manner. This helps to develop a better intuitive understanding of the often complex evolutionary dynamics and encourage further explorations in the fascinating and often mesmerizing world of spatio-temporal patterns. | ||
| Line 12: | Line 12: | ||
</div> | </div> | ||
<div class=" | == Tutorials == | ||
=== [[Mutualisms: cooperation between species|Symmetry breaking of cooperation between species]] === | |||
{| | |||
| style="vertical-align:top" |[[Image:Mutualism two-layer lattice.png|160px|left|link= Mutualisms: cooperation between species]] | |||
| style="vertical-align:top" | | |||
Tutorial on [[Mutualisms: cooperation between species|''inter-species interactions'']]. | |||
Cooperative interactions ''between'' species are the foundation of all mutualistic associations. Compared to ''within'' species interactions, the problem of cooperation is exacerbated because cooperation bestows benefits to members of another species. Mutual benefits require inter-species coordination to prevent exploitation. Here we show that in the spatial prisoner's dilemma surprisingly rich dynamics emerge with distinct dynamical domains separated by critical phase transitions, which imply arbitrarily large fluctuations and diverging spatial correlations. Most importantly, cooperative behaviour not only persists, but may result in intriguing, spontaneous symmetry breaking in the level of cooperation in each species. Evolution may favour asymmetric states that effectively separate species into cooperative producers and defecting consumers. Surprisingly, the asymmetry becomes more pronounced under more benign conditions of cooperation. | |||
<div class="footnote" style="font-size:smaller"> | |||
Hauert, C., & Szabó, G. (2024) ''PNAS Nexus'' '''3''' 9 pgae326 [https://doi.org/10.1093/pnasnexus/pgae326 doi: 10.1093/pnasnexus/pgae326] | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[Spatial social dilemmas promote diversity]] === | |||
{| | |||
| style="vertical-align:top" |[[Image:Spatial social dilemmas promote diversity.jpg|160px|left|link=Spatial social dilemmas promote diversity]] | |||
| style="vertical-align:top" | | |||
Tutorial on [[Spatial social dilemmas promote diversity|modes of spontaneous diversification in spatial settings]]. | |||
Evolutionary branching and diversification in interactions with continuous behavioural traits is important for understanding the emergence of distinct, discrete, and coexisting strategies. In social dilemmas, this suggests an evolutionary pathway for the origin of cooperators and defectors. Here we study evolutionary diversification in structured populations and identify mechanisms driving spontaneous and persistent diversification. We develop a [[spatial adaptive dynamics]] framework by combining adaptive dynamics and pair approximation to capture local correlations arising from spatial extensions. Through analytical and numerical techniques, we demonstrate that spatial structure admits new modes of diversification that complement classical evolutionary branching. In particular, when selection is strong, diversification tends to occur more readily than in unstructured populations. | |||
<div class="footnote" style="font-size:smaller"> | |||
Hauert, C., & Doebeli, M. (2021) ''PNAS'' '''118''' 42 e2105252118 [https://doi.org/10.1073/pnas.2105252118 doi: 10.1073/pnas.2105252118]. | |||
</div> | |||
|} | |||
{{-}} | |||
=== Spatial games: interaction and competition neighbourhoods === | |||
{| | |||
| style="vertical-align:top" |[[Image:Lattice.png|160px|left|link=Spatial games: interaction and competition neighbourhoods]] | |||
| style="vertical-align:top" | | |||
''Upcoming:'' new tutorial on <!--[[Spatial games: interaction and competition neighbourhoods|-->''overlapping versus disjoint neighbourhoods''<!--]]--> in the spatial donation game. Traditionally the interaction and competition neighbourhoods are identical. Here we discuss intriguing differences in the dynamics that arise when separating the neighbourhoods to nearest neighbour interactions and second nearest neighbour competition. On square lattices this results in two equivalent disjoint sub-lattices for competition. The extinction of cooperators for higher cost-to-benefit ratios r remains the same in both scenarios and exhibits a critical phase transition with characteristics of directed percolation. Intriguingly, for smaller r, distinct levels of cooperation can emerge in the two sub-lattices through spontaneous symmetry breaking, which resembles the sub-lattice ordering in the anti-ferromagnetic Ising model. Decreasing r further, induces extremely large fluctuations (bursts) in the frequencies of cooperation. These bursts eventually drive the system into one of the absorbing states: occasionally homogeneous defection in both sub-lattices but usually only in one and homogeneous cooperation in the other, achieving perfect asymmetry. This is in stark contrast to the traditional case where cooperation keeps increasing as r decreases and conditions become more benign. | |||
<div class="footnote" style="font-size:smaller"> | |||
Hauert, C., & Szabó, G. (2025) ''under review'' <!--''Phys. Rev. E'' '''X''' Y Z [https://doi.org/ doi: ]--> | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[Evolutionary graph theory]] === | |||
{| | |||
| style="vertical-align:top" |[[Image:Superstar graph (N=484, B=21, k=6).svg|160px|left|link=Evolutionary graph theory]] | |||
| style="vertical-align:top" |Tutorial on [[evolutionary graph theory]], which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in structured populations. Interestingly, the fixation probabilities remain unaffected by the underlying structure for a [[Moran graphs|large class of graphs]]. However, some graphs may act either as [[Evolutionary amplifiers|amplifiers]] or [[Evolutionary suppressors|suppressors]] of selection by increasing or decreasing the fixation probabilities as compared to unstructured populations. In contrast, fixation and absorption times are very sensitive to changes in the graph structure and hence vary greatly even for graphs that leave fixation probabilities unchanged. Even though fixation times are, in general, not preserved between graphs, [[Graph symmetries|symmetries of a graph]] can at least ensure that fixation times do not depend on the initial location of the mutant. This summarizes research efforts that span over a decade, including: | |||
<div class="footnote" style="font-size:smaller"> | |||
#Lieberman, E., Hauert, C. & Nowak, M. (2005) ''Nature'' '''433''' 312-316 [http://dx.doi.org/10.1038/nature03204 doi: 10.1038/nature03204]. | |||
#Jamieson-Lane, A. & Hauert, C. (2015) ''J. Theor. Biol.'' '''382''' 44-56 [http://dx.doi.org/10.1016/j.jtbi.2015.06.029 doi: 10.1016/j.jtbi.2015.06.029]. | |||
#McAvoy, A. & Hauert, C. (2015) ''J. R. Soc. Interface'' '''12''' 20150420 [http://dx.doi.org/10.1098/rsif.2015.0420 doi: 10.1098/rsif.2015.0420] | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[Stochastic dynamics in finite populations]] === | |||
{| | |||
| style="vertical-align:top" |[[Image:RSP - SDE.svg|160px|left|link=Stochastic dynamics in finite populations]] | |||
| style="vertical-align:top" |Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations. | |||
<div class="footnote" style="font-size:smaller"> | |||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2012) ''Phys. Rev. E'' '''85''' 041901 [http://dx.doi.org/10.1103/PhysRevE.85.041901 doi: 10.1103/PhysRevE.85.041901]. | |||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2006) ''Phys. Rev. E'' '''74''' 011901 [http://dx.doi.org/10.1103/PhysRevE.74.011901 doi: 10.1103/PhysRevE.74.011901]. | |||
#Traulsen, A., Claussen, J. C. & Hauert, C. (2005) ''Phys. Rev. Lett.'' '''95''' 238701 [http://dx.doi.org/10.1103/PhysRevLett.95.238701 doi: 10.1103/PhysRevLett.95.238701]. | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[Evolutionary Games and Population Dynamics]] === | |||
{| | |||
| style="vertical-align:top" | [[Image:Evolutionary games and population dynamics.gif|left|160x160px|link=Evolutionary Games and Population Dynamics]] | |||
| style="vertical-align:top" |Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups. | |||
<div class="footnote" style="font-size:smaller"> | |||
# Wakano, J. Y. & Hauert, Ch. (2011) J. theor. Biol. 268 30-38 [http://dx.doi.org/10.1016/j.jtbi.2010.09.036 doi: 10.1016/j.jtbi.2010.09.036]. | |||
# Wakano, J. Y., Nowak, M. A. & Hauert, Ch. (2009) Proc. Natl. Acad. Sci. USA 106 7910-7914 [http://dx.doi.org/10.1073/pnas.0812644106 doi: 10.1073/pnas.0812644106]. | |||
# Hauert, Ch., Wakano, J. Y. & Doebeli, M. (2008) Theor. Pop. Biol. '''73''', 257-263 [http://dx.doi.org/10.1016/j.tpb.2007.11.007 doi:10.1016/j.tpb.2007.11.007]. | |||
# Hauert, C., Holmes, M. & Doebeli, M. (2006) Proc. R. Soc. Lond. B '''273''', 2565-2570 [http://dx.doi.org/10.1098/rspb.2006.3600 doi: 10.1098/rspb.2006.3600]. | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[Origin of Cooperators and Defectors]] === | |||
{| | |||
| style="vertical-align:top" |[[Image:Origin of cooperators and defectors.gif|left|160x160px|link=Origin of Cooperators and Defectors]] | |||
| style="vertical-align:top" |Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial. | |||
<div class="footnote" style="font-size:smaller"> | |||
# Killingback, T., Doebeli, M. & Hauert, Ch. (2010) Biological Theory 5, 3-6 [http://dx.doi.org/10.1162/BIOT_a_00019 doi: 10.1162/BIOT_a_00019]. | |||
# Doebeli, M., Hauert, C. & Killingback, T. (2004) Science '''306''', 859-862 [http://dx.doi.org/10.1126/science.1101456 doi: 10.1126/science.1101456]. | |||
</div> | |||
|} | |||
{{-}} | |||
=== [[2×2 Games]] === | |||
{| | |||
| style="width:160px; text-align:center; vertical-align:top" | [[Image:Cover IJBC 2002.12.png|center|160x160px|link=2×2 Games]] | |||
| style="vertical-align:top" | Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world. | |||
<div class="footnote" style="font-size:smaller"> | |||
# Hauert, C. (2002) Int. J. of Bifurcation & Chaos '''12''' 1531-1548 [http://dx.doi.org/10.1142/S0218127402005273 doi: 10.1142/S0218127402005273]. | |||
# Hauert, C. (2001) Proc. R. Soc. Lond. B 268, 761-769 [http://dx.doi.org/10.1098/rspb.2000.1424 doi: 10.1098/rspb.2000.1424]. | |||
</div> | |||
|} | |||
{{-}} | |||
<!-- | |||
== [[Introduction]] == | |||
[[Image:Founding fathers of Game Theory.gif|left|border|160x160px]] | |||
Quick introduction covering the basic ideas of evolutionary game theory illustrated with many examples. This section briefly introduces classic games such as the Prisoner's Dilemma, the Hawk-Dove- or Snowdrift game and the Rock-Scissors-Paper game. It is intended as an overview of the many features and capabilities of the interactive ''EvoLudo'' simulator. | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Via freedom to coercion: the emergence of costly punishment]] == | |||
[[Image:Via freedom to coercion.gif|left|160x160px]] | |||
Tutorial on the role of voluntary participation in joint effort games for the evolution of costly punishing behavior. The freedom to withdraw from common enterprises leads to the enforcement of social norms. Joint enterprises which are compulsory rather than voluntary are less likely to lead to cooperation. | |||
<div class="footnote"> Hauert, C., Traulsen, A., Brandt, H., Nowak, M. A. & Sigmund, K. (2007) ''Via freedom to coercion: the emergence of costly punishment,'' ''Science'' '''316''', 1905-1907. </div> | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Synergy & discounting of cooperation in social dilemmas]] == | |||
[[Image:Synergy & discounting in social dilemmas.gif|left|160x160px]] | |||
Tutorial on cooperation in social dilemmas. Social dilemmas are characterized by a conflict of interest between the individuals and the group. The most prominent examples of social dilemmas are the prisoner's dilemma, the snowdrift game and public goods game. Based on the concept of synergistic or discounted accumulation of cooperative benefits we present a unifying framework to model cooperation in social dilemmas. | |||
<div class="footnote"> Hauert, C., Michor, F., Nowak, M. & Doebeli, M. (2006) J. theor. Biol. '''239''', 195-202.<br /> Hauert, C. (2006) J. theor. Biol. '''240''', 627-636. </div> | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Cooperation in structured populations]] == | |||
[[Image:Cooperation in structured populations.gif|left|border|160x160px]] | |||
Tutorial on the fate of cooperative behavior in two closely related evolutionary games: the Prisoner's Dilemma and the Snowdrift (Hawk-Dove) game. The population structure then determines whether the evolution and maintenance of cooperation is promoted or hindered. In particular, this interactive tutorial illustrates that, in contrast to the Prisoner's Dilemma, spatial structure can be detrimental to cooperation in the Snowdrift game. | |||
<div class="footnote"> Hauert, C. & Doebeli, M. (2004) Nature '''428''', 643-646. </div> | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Voluntary Public Goods Games]] == | |||
[[Image:Voluntary Public Goods Games.gif|left|border|160x160px]] | |||
Tutorial on voluntary participation in public goods games. Most of the literature on cooperation in social dilemmas assumes that interactions are compulsory. In most real-life situations, however, individuals may choose to opt out whenever a public enterprise appears too risky. This results in a rock-scissors-paper type dominance of cooperators, defectors and loners (those that do not participate). Volunteering can maintain cooperation in mixed populations and results in fascinating spatio-temporal patterns in spatial settings. | |||
<div class="footnote"> Hauert, C., De Monte, S., Hofbauer, J. & Sigmund, K. (2002) Science '''296''' 1129-1132.<br /> Hauert, C., De Monte, S., Hofbauer, J. & Sigmund, K. (2002) J. theor. Biol. '''218''' 187-194. </div> | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Public goods games]] == | |||
[[Image:Public goods games.gif|left|border|160x160px]] | |||
Tutorial on public goods games in populations with different structures. Public goods games essentially represent a generalization of the pairwise prisoner's dilemma interactions to groups of arbitrary size. In spatially extended populations, where individuals interact within a limited local neighborhood, cooperators can persist through cluster formation. Variations of the value of the public good result in a critical phase transition which relates to percolation phenomena from condensed matter physics. | |||
<div class="footnote"> Szabó, G. & Hauert, C. (2002) Phys. Rev. Lett. '''89''' (11) 118101. </div> | |||
{{-}} | |||
--> | |||
<!-- | |||
== [[Reward, punishment and reputation]] == | |||
[[Image:Reward, punishment & reputation.gif|left|border|160x160px]] | |||
Tutorial on effects of reward, punishment and reputation in Public Goods games. Various experimental studies on social dilemmas have shown that punishment is very efficient in creating incentives for cooperative behavior. Reward, however, is considerably less efficient. The underlying mechanisms are illustrated with a simple game theoretical model. | |||
<div class="footnote"> Sigmund, K., Hauert, C. & Nowak, M. (2001) Proc. Natl Acad. Sci. USA '''98''', 10757-10762.<br /> Brandt, H., Hauert, C. & Sigmund, K. (2003) Proc. R. Soc. Lond. B '''270''', 1099-1104. </div> | |||
{{-}} | |||
--> | |||
== News == | |||
'''March 2025''' New tutorial on [[Spatial social dilemmas promote diversity]] added to interactively explore the results reported in Hauert & Doebeli (2021) ''PNAS'' '''118''' (42) e2105252118 [https://doi.org/10.1073/pnas.2105252118 doi: 10.1073/pnas.2105252118] | |||
'''January 2025''' ''EvoLudo'' simulation toolkit released into the public domain and is available on [https://www.github.com/evoludolab/EvoLudo GitHub] and has a doi for citations: [https://doi.org/10.5281/zenodo.14591550 10.5281/zenodo.14591550]. Pull requests are encouraged and welcome! | |||
'''September 2024''' New tutorial on [[Mutualisms: cooperation between species|cooperation ''between'' species]] added to interactively explore the results reported in Hauert & Szabó, ''PNAS Nexus'' '''3''' (9) pgae326 [https://doi.org/10.1093/pnasnexus/pgae326 doi: 10.1093/pnasnexus/pgae326] | |||
'''August 2024''' MediaWiki software updated and looks modernized. ''EvoLudo'' simulations updated. | '''August 2024''' MediaWiki software updated and looks modernized. ''EvoLudo'' simulations updated. | ||
'''October 2023''' ''EvoLudo'' simulation toolkit extended and MediaWiki software updated and general maintenance. [https://www.evoludo.org/docs/api The API documentation] of the ''EvoLudo'' simulation toolkit is now available. Plans to release the source code into the public domain are in progress - stay tuned. | '''October 2023''' ''EvoLudo'' simulation toolkit extended and MediaWiki software updated and general maintenance. [https://www.evoludo.org/docs/api The API documentation] of the ''EvoLudo'' simulation toolkit is now available. Plans to release the source code into the public domain are in progress - stay tuned. | ||
'''October 2016''' ''EvoLudo'' simulation toolkit updated. The simulations are now resizable | '''October 2016''' ''EvoLudo'' simulation toolkit updated. The simulations are now resizable and fullscreen is improved (still beta, though). Moreover, snapshots of views and statistical data can be exported through the context menu. | ||
'''August 2016:''' New tutorial on [[evolutionary graph theory]] added. This includes significant extensions and improvements of the ''EvoLudo'' labs to do statistical analysis over several simulation runs to determine fixation probabilities and fixation times. | '''August 2016:''' New tutorial on [[evolutionary graph theory]] added. This includes significant extensions and improvements of the ''EvoLudo'' labs to do statistical analysis over several simulation runs to determine fixation probabilities and fixation times. | ||
| Line 23: | Line 191: | ||
'''June 2016:''' 3D capabilities added to the interactive ''EvoLudo'' labs using WebGL! Check out the 3D representations of population structures. If you have your red-cyan glasses ready, the structures can be viewed even in real 3D (use context menu). In addition some fullscreen capabilities have been added but this feature is still under construction - stay tuned. | '''June 2016:''' 3D capabilities added to the interactive ''EvoLudo'' labs using WebGL! Check out the 3D representations of population structures. If you have your red-cyan glasses ready, the structures can be viewed even in real 3D (use context menu). In addition some fullscreen capabilities have been added but this feature is still under construction - stay tuned. | ||
'''March 2016:''' ''EvoLudo'' revamped! Java applets have been retired and | '''March 2016:''' ''EvoLudo'' revamped! Java applets have been retired and replaced by a JavaScript implementation generated by [https://www.gwtproject.org GWT]. As a welcome side-effect, the interactive tutorials are now finally also accessible from tablets and other mobile devices. This major update of the ''EvoLudo'' simulation and visualization framework has been made possible through my sabbatical leave from [https://www.math.ubc.ca UBC] and facilitated by an extended research visit of [https://www.evolbio.mpg.de/5868/group_theoreticalbiology Arne Traulsen's group] at the [https://www.evolbio.mpg.de Max-Planck Institute for Evolutionary Biology] in Plön, Germany. | ||
{{-}} | {{-}} | ||
<!-- | |||
<div class="mainpage_hubtitle">'''Recent'''</div> | <div class="mainpage_hubtitle">'''Recent'''</div> | ||
<div class="mainpage_boxcontents"> | <div class="mainpage_boxcontents"> | ||
| Line 31: | Line 200: | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
--> | |||
== Highlights == | |||
{{EvoLudo/Highlights}} | {{EvoLudo/Highlights}} | ||
{{-}} | {{-}} | ||
Latest revision as of 15:11, 7 March 2025
EvoLudo is a growing collection of interactive tutorials that complement numerous research articles on evolutionary games (ludo Latin for "I play" or Italian for "game"). These tutorials allow the reproduction and verification of results reported in scientific articles. In addition, they are intended to encourage the interested reader, students and researchers to explore the fascinating world of game theory and evolutionary dynamics in a playful manner. This helps to develop a better intuitive understanding of the often complex evolutionary dynamics and encourage further explorations in the fascinating and often mesmerizing world of spatio-temporal patterns.
In 2012 the EvoLudo wiki was introduced as the successor of the VirtualLabs, which were originally hosted by the University of Vienna. The VirtualLabs pages have been retired partly because the interactive tutorials were based on the long obsolete technology of java applets. The adventurous and fearless are welcome to visit the archived pages. Over the 10 years since their initial instalment in 2002 the VirtualLabs have attracted over 250k visitors (which was significant back in the day).
The VirtualLabs, and EvoLudo by extension, have been encouraged and inspired by Karl Sigmund during my post-doc under his mentorship.
The EvoLudo wiki is created and maintained by Christoph Hauert. Feedback, suggestions and contributions are most welcome.
Tutorials
Symmetry breaking of cooperation between species
 |
Tutorial on inter-species interactions. Cooperative interactions between species are the foundation of all mutualistic associations. Compared to within species interactions, the problem of cooperation is exacerbated because cooperation bestows benefits to members of another species. Mutual benefits require inter-species coordination to prevent exploitation. Here we show that in the spatial prisoner's dilemma surprisingly rich dynamics emerge with distinct dynamical domains separated by critical phase transitions, which imply arbitrarily large fluctuations and diverging spatial correlations. Most importantly, cooperative behaviour not only persists, but may result in intriguing, spontaneous symmetry breaking in the level of cooperation in each species. Evolution may favour asymmetric states that effectively separate species into cooperative producers and defecting consumers. Surprisingly, the asymmetry becomes more pronounced under more benign conditions of cooperation. Hauert, C., & Szabó, G. (2024) PNAS Nexus 3 9 pgae326 doi: 10.1093/pnasnexus/pgae326 |
Spatial social dilemmas promote diversity
 |
Tutorial on modes of spontaneous diversification in spatial settings. Evolutionary branching and diversification in interactions with continuous behavioural traits is important for understanding the emergence of distinct, discrete, and coexisting strategies. In social dilemmas, this suggests an evolutionary pathway for the origin of cooperators and defectors. Here we study evolutionary diversification in structured populations and identify mechanisms driving spontaneous and persistent diversification. We develop a spatial adaptive dynamics framework by combining adaptive dynamics and pair approximation to capture local correlations arising from spatial extensions. Through analytical and numerical techniques, we demonstrate that spatial structure admits new modes of diversification that complement classical evolutionary branching. In particular, when selection is strong, diversification tends to occur more readily than in unstructured populations. Hauert, C., & Doebeli, M. (2021) PNAS 118 42 e2105252118 doi: 10.1073/pnas.2105252118. |
Spatial games: interaction and competition neighbourhoods
Evolutionary graph theory
 |
Tutorial on evolutionary graph theory, which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in structured populations. Interestingly, the fixation probabilities remain unaffected by the underlying structure for a large class of graphs. However, some graphs may act either as amplifiers or suppressors of selection by increasing or decreasing the fixation probabilities as compared to unstructured populations. In contrast, fixation and absorption times are very sensitive to changes in the graph structure and hence vary greatly even for graphs that leave fixation probabilities unchanged. Even though fixation times are, in general, not preserved between graphs, symmetries of a graph can at least ensure that fixation times do not depend on the initial location of the mutant. This summarizes research efforts that span over a decade, including:
|
Stochastic dynamics in finite populations
 |
Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations.
|
Evolutionary Games and Population Dynamics
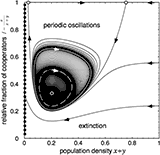 |
Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups.
|
Origin of Cooperators and Defectors
 |
Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial.
|
2×2 Games
 |
Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world.
|
News
March 2025 New tutorial on Spatial social dilemmas promote diversity added to interactively explore the results reported in Hauert & Doebeli (2021) PNAS 118 (42) e2105252118 doi: 10.1073/pnas.2105252118
January 2025 EvoLudo simulation toolkit released into the public domain and is available on GitHub and has a doi for citations: 10.5281/zenodo.14591550. Pull requests are encouraged and welcome!
September 2024 New tutorial on cooperation between species added to interactively explore the results reported in Hauert & Szabó, PNAS Nexus 3 (9) pgae326 doi: 10.1093/pnasnexus/pgae326
August 2024 MediaWiki software updated and looks modernized. EvoLudo simulations updated.
October 2023 EvoLudo simulation toolkit extended and MediaWiki software updated and general maintenance. The API documentation of the EvoLudo simulation toolkit is now available. Plans to release the source code into the public domain are in progress - stay tuned.
October 2016 EvoLudo simulation toolkit updated. The simulations are now resizable and fullscreen is improved (still beta, though). Moreover, snapshots of views and statistical data can be exported through the context menu.
August 2016: New tutorial on evolutionary graph theory added. This includes significant extensions and improvements of the EvoLudo labs to do statistical analysis over several simulation runs to determine fixation probabilities and fixation times.
June 2016: 3D capabilities added to the interactive EvoLudo labs using WebGL! Check out the 3D representations of population structures. If you have your red-cyan glasses ready, the structures can be viewed even in real 3D (use context menu). In addition some fullscreen capabilities have been added but this feature is still under construction - stay tuned.
March 2016: EvoLudo revamped! Java applets have been retired and replaced by a JavaScript implementation generated by GWT. As a welcome side-effect, the interactive tutorials are now finally also accessible from tablets and other mobile devices. This major update of the EvoLudo simulation and visualization framework has been made possible through my sabbatical leave from UBC and facilitated by an extended research visit of Arne Traulsen's group at the Max-Planck Institute for Evolutionary Biology in Plön, Germany.
Highlights

|
ClassicsClassic patterns generated by the spatial prisoner's dilemma and first published by Nowak, M. A. & May, R. M. Nature 359 826-829 (1992). Spatial structure enables cooperators (blue, green) survive under conditions where otherwise defectors (red, yellow) would take over. Through spatial clustering cooperators interact more frequently with other cooperators and reduce exploitation by defectors. |

|
ModernSpatial heterogeneity promotes cooperation based on different types of pattern formation processes driving the density distribution of cooperators (green) and defectors (red). Individuals can migrate (diffuse) in order to populate empty territories (black). Slow diffusion of cooperators fosters aggregation in highly productive patches (activation), whereas fast diffusion enables defectors to readily locate and exploit these patches (inhibition). These antagonistic forces promote co-existence of cooperators and defectors in static or dynamic patterns, including spatial chaos of ever changing configurations |

|
ArtsInstallation "Evolution" on the NOVA, the world's largest true 3D display in the main train station in Zürich, Switzerland. The installation was created in collaboration with media artist Chandrasekhar Ramakrishnan and is based on the EvoLudo simulation toolkit. “Evolution” was presented in September 2009 in honour of Darwin's bicentenary and became part of the permanent collection until NOVA was retired in 2012. The NOVA display is a 5×5×1m cube of 25,000 LED lights and displays the competition of cooperators (blue, green) and defectors (red, yellow) in the prisoner’s dilemma in 3D unfolding as an evolutionary kaleidoscope. |