Origin of Cooperators and Defectors
Traditionally in both classical as well as evolutionary game theory a finite set of discrete strategies is assumed a priori. When discussing the evolution of cooperation in social dilemmas, the simplest set of strategies would consist of cooperators and defectors. Cooperators provide a benefit to other individuals at some cost, while defectors attempt to exploit such common resources. This leads to a classic conflict of interest between the individual's and the community performance - and hence the dilemma. The game dynamics then determines the relative frequencies of the different strategies in a population.
From an evolutionary perspective, however, it is essential to understand the emergence of discrete strategies and particularly of cooperators and defectors in order to justify these a priori assumptions. Since evolution is a gradual process, it is important to consider continuous variants of game theoretical metaphors for cooperative interactions such as the Prisoner's Dilemma or the Snowdrift game. The essential difference between the two games is that in the Prisoner's Dilemma the benefits of cooperation accrue exclusively to the other individuals whereas in the Snowdrift game the act of cooperation also provides some benefits to the cooperator itself.
Even though the Snowdrift game has received relatively little attention in the literature it appears to be highly relevant in many biologically scenarios: Consider for example Saccharomyces cerevisiae a single-celled yeast species. The yeast cells secrete an enzyme which 'digests' their immediate surroundings (invertase hydrolyzes sucrose) and turns it into a food resource. Since this food resource is commonly available, it represents a public good that can be easily exploited by defectors that produce little or no enzyme (but rather reproduce faster). However, if no one produces the enzyme, everybody will die of starvation. Therefore, the costs and benefits of cooperative investments crucially depend on the present environment.
This tutorial complements a series of research articles by Michael Doebeli, Timothy Killingback & Christoph Hauert
Continuous Snowdrift game
Let us assume two individuals with strategies \(x\) and \(y\). The payoff of \(x\) interacting with \(y\) could then be written as \(P(x,y) = B(x+y)-C(x)\) where the benefit \(B(x+y)\) depends on the accumulated investments made (i.e. the total amount of enzyme produced) while the incurring costs \(C(x)\) obviously only depend on the investment \(x\).
In the following we highlight the rich and intriguing dynamics arising from this simple model. In particular, we demonstrate that this scenario can easily lead to evolutionary branching which gives rise to the spontaneous emergence of discrete strategies, i.e. cooperators and defectors. The two strategies co-exist in a stable equilibrium even under strictly mixing conditions and in absence of assortative interactions.
In the simplest case with \(B(x+y) = b_2(x+y)^2+b_1(x+y)\) and \(C(x) = c_2 x^2+c_1 x\) the system can be fully analyzed and the dynamics is characterized by five different scenarios. Note that quadratic functions are the simplest interesting ones - with \(B(x+y)\) and \(C(x)\) linear, the dynamics is rather uninteresting and dull.
All of the following examples and suggestions are meant as inspirations for further experiments. Each example opens a new page with a running lab with all necessary parameters set as appropriate to demonstrate the different scenarios.
Evolutionary dynamics if singular strategy exists

Attractor - convergent stable and evolutionarily stable
Provided that the equilibrium \(x^*\) exists, the singular strategy \(x^*\) is an attractor if \(2b_2 < c_2 < b_2 < 0\) holds. In that case, any monomorphic population will converge to \(x^*\) and remain there at intermediate cooperative investment levels. This outcome is independent of the initial strategy \(x_0\). The time evolution is illustrated in the figure to the left. The abscissa denotes the trait \(x\) and the ordinate represents time (in Monte Carlo steps). Darker shades of grey specify higher abundance of individuals with a particular trait. White regions indicate the absence of a particular trait in the population.
Such stable intermediate investment levels are related to results for the Snowdrift (or Hawk-Dove) game with mixed strategies, i.e. where individuals have a certain probability to cooperate or defect. In equilibrium, an intermediate propensity to cooperate evolves and represents an evolutionarily stable state.

Branching point - convergent stable but not evolutionarily stable
If \(x^*\) still exists but only \(2 b_2 < c_2 < 0\) holds for convergent stability but not \(c_2 < b_2 < 0\) for evolutionary stability, truly fascinating dynamics occur: First, any monomorphic population evolves towards \(x^*\) but now \(x^*\) represents a fitness minimum and so adjacent strategies can invade which leads to evolutionary branching. Despite random interactions, spontaneously low and high investing traits evolve. For quadratic functions, it can be shown, that the two branches diverge until they reach the boundary of the trait space, i.e. evolution ends with a stable mixture of pure cooperators (maximum investments) and pure defectors (minimum investments).

Repellor - not convergent stable
If \(x^*\) exists but \(2b_2 < c_2 < 0\) is violated, i.e. \(x^*\) is not convergent stable, then \(x^*\) is called a repellor because the population evolves away from \(x^*\). This is a bi-stable situation. Depending on the initial strategy \(x_0\), the population evolves to all defectors (\(x_0 < x^*\)) or all cooperators (\(x_0 > x^*\)). Note that \(x^*\) could still be an evolutionarily stable strategy, however, this would be quite irrelevant since \(x^*\) would be never reached without careful preparation of the initial configuration.
The figure combines two different simulation runs, one for \(x_0 < x^*\) where investments decrease and another for \(x_0 > x^*\) where they reach their maximum.
Evolutionary dynamics in the absence of singular strategies

Dominance (defection)
If the benefit that accrues to the cooperator itself is insufficient to cover the incurring costs in absence of cooperating co-players then defection dominates and lower investing individuals are better off. Consequently, the investment levels decrease and cooperation vanishes - despite the fact that everybody would be better off cooperating. This situation corresponds to the strictest form of a social dilemma and relates to the continuous Prisoner's Dilemma.

Dominance (cooperation)
In contrast to the Prisoner's Dilemma, mutualistic interactions represent the weakest form of a social dilemma. In fact, here cooperation dominates, i.e. higher investing individuals thrive. In a game theoretical setting assume a group of cooperators a and a single defector. The defector still outperforms the cooperators because he/she avoids the incurring costs. However, in a mutualistic setting, the defector would have been even better off by switching to cooperation too. As a consequence cooperative investments increase over time until they reach the upper limit.
Evolutionary dynamics of more complex scenarios

Branching point and repellor
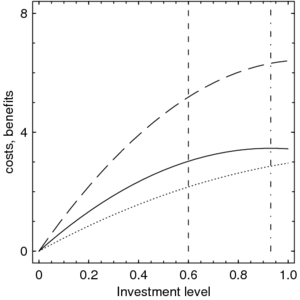
More complicated cost and benefit functions lead to very interesting dynamics but generally they make a complete analysis impossible. Here we set \(B(x) = b \sqrt{(x+y)}\) and \(C(x) = \ln(c x+1)\). This may lead to the simultaneous occurrence of a branching point and a repellor. The results are summarized in the figure to the left. Starting to the left of the repellor (dash-dotted vertical line) investments decrease until they reach the branching point (dashed vertical line) and then two strategies co-exist and diverge until the upper branch reaches the maximum investment, i.e. hits the boundary of the trait range. Note that the dimorphic population after the branching point does no longer 'see' the repellor near \(x = 4\). The small inset show another simulation run starting to the right of the repellor. The trait simply increases until it hits the boundary.

Branching point and repellor - intermediate investment levels
So far, whenever branching occurred the upper branch, i.e. investments increased until they reached the boundary of the trait range. In order to illustrate that this must not be the case consider \(B(x+y) = b (1-\exp(-x))\) and \(C(x) = \ln(c x+1)\). As shown in the figure to the left, it may now occur that initially high investment levels decrease until the branching point is reached and then the upper branch reaches saturation around \(x = 2.1\). The fact that at low \(x\) there exists also a repellor becomes evident only when starting with very small \(x_0\). In that case the trait quickly reaches zero and remains there as shown in the little inset.
Adaptive dynamics in a nutshell
Consider a monomorphic population with strategy \(x\). The growth rate of a rare mutant \(y\) in the resident population \(x\) is determined by \begin{align} f_x(y) &= P(y,x)-P(x,x)\\ &= B(x+y)-C(y)-(B(2x)-C(x)). \end{align} The evolution of trait \(x\) is then given by \begin{align} \frac{dx}{dt} = D(x) = \frac{df_x}{dy}\bigg|_{y=x} = B^\prime(2x)-C^\prime(x), \end{align} i.e. \(D(x) = 4 b_2 x+b_1-2 c_2 x-c_1\). If an equilibrium \(x^*\) with \(D(x^*)=0\) exists, it is called a convergent stable strategy (CSS) if \begin{align} \frac{dD}{dx}\bigg|_{x=x^*} = 2 B^{\prime\prime}(2 x^*)-C^{\prime\prime}(x^*)<0, \end{align} which reduces to \(2b_2-c_2 <0\) for quadratic cost- and benefit functions. Otherwise, \(x^*\) is a repellor. Interestingly, the CSS condition does not imply evolutionary stability of \(x^*\). Instead, evolutionary stability requires that \(x^*\) is a maximum of \(f_x\), i.e. \begin{align} \frac{d^2 f_x}{dy^2}\bigg|_{y=x^*}<0 \end{align} or \(b_2-c_2<0\). If this does not hold \(x^*\) is a branching point\((2 b_2 < c_2 < b_2 < 0)\) because mutants on both sides of \(x^*\) can invade, which then results in spontaneous diversification.
References
- Killingback, T., Doebeli, M. & Hauert, C. (2010) Cooperation and Defection in the Tragedy of the Commons, Biological Theory 5, 3-6 doi: 10.1162/BIOT_a_00019.
- Doebeli, M., Hauert, C. & Killingback, T. (2004) The evolutionary origin of cooperators and defectors, Science 306, 859-862 doi: 10.1126/science.1101456.
Press & News
- When Laziness Pays: Math explains how cooperation and cheating evolve (2005) ScienceNews 167 (3) 35 by Erika Klarreich (January 15).
- Egoismo e altruismo, sempre in equilibrio (2004) Il Corriere della Sera (October 31) by Massimo Piattelli Palmarini.
This article 'Egoism and altruism, always in equilibrium' appeared in an Italian national newspaper. - Warum einige immer abräumen und andere ständig draufzahlen (2004) Die Welt (November 22) by Ranty Islam.
This article 'Why some always scoop the market and others persistently overpay' appeared in a German national newspaper.
Acknowledgements
These fascinating research results would have never been achieved without the inspiring discussions and advice from Michael Doebeli and Timothy Killingback. The evolutionary origin of this collection of tutorials lies in Karl Sigmund's encouragement, scientific inspiration and advice. To conquer the tricky subtleties of Java the patience and competence of Urs Bill was invaluable. Financial support of the Swiss National Science Foundation is gratefully acknowledged.
