Spatial social dilemmas promote diversity: Difference between revisions
No edit summary |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
=== Continuous Donation game === | === Continuous Donation game === | ||
A natural translation of the donation game to continuous traits is based on cost and benefit functions, \(C(x)\) and \(B(x)\), where the trait \(x\in[0,x_\text{max}]\) represents a level of cooperative investment that can vary continuously. In the spirit of the donation game, an individual with strategy \(x\) interacting with an \(y\)-strategist obtains a payoff \(P(x,y)=B(y)-C(x)\). Assuming that | A natural translation of the donation game to continuous traits is based on cost and benefit functions, \(C(x)\) and \(B(x)\), where the trait \(x\in[0,x_\text{max}]\) represents a level of cooperative investment that can vary continuously. In the spirit of the donation game, an individual with strategy \(x\) interacting with an \(y\)-strategist obtains a payoff \(P(x,y)=B(y)-C(x)\). Assuming that | ||
# zero investments incur no costs and provide no benefits, \(B(0)=C(0)=0\), | |||
# benefits exceed costs, \(B(x)>C(x)\geq0\), and | |||
# are increasing functions, \(B^\prime(x), C^\prime(x)\geq0\), | |||
recovers the social dilemma of the donation game for continuous investment levels: the level of investment invariably evolves to zero, which corresponds to pure defection, despite the fact that both players would be better off at non-zero investment levels. The reason is that an actor can only influence the cost \(C(x)\) of an interaction, but not the received benefit \(B(y)\), and hence selection can only act to minimize costs. | |||
=== Continuous Snowdrift game === | === Continuous Snowdrift game === | ||
| Line 17: | Line 21: | ||
== Evolution in the continuous prisoner's dilemma == | == Evolution in the continuous prisoner's dilemma == | ||
In the continuous prisoner's dilemma the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x)-C(y)\). This implies that the selection gradient in well-mixed populations is proportional to \(-C'(x)\), and hence, assuming monotonously increasing costs, no singular strategy exists apart from the pure defection state \(x=0\), and the population always evolves to that state, regardless of how large the benefits of cooperation are. In contrast, for death-birth updating in structured populations the selection gradient | In the continuous prisoner's dilemma the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x)-C(y)\). This implies that the selection gradient in well-mixed populations is proportional to \(-C'(x)\), and hence, assuming monotonously increasing costs, no singular strategy exists apart from the pure defection state \(x=0\), and the population always evolves to that state, regardless of how large the benefits of cooperation are. In contrast, for death-birth updating in structured populations the selection gradient for [[spatial adaptive dynamics]] becomes | ||
\begin{align} | \begin{align} | ||
\label{eq:d:pd:dB} | \label{eq:d:pd:dB} | ||
D_\text{db}(x) &= w\frac{k-2}{k(k-1)}(B^\prime(x)-k C^\prime(x)). | D_\text{db}(x) &= w\frac{k-2}{k(k-1)}(B^\prime(x)-k C^\prime(x)). | ||
\end{align} | \end{align} | ||
Thus, in structured populations a singular strategy, \(x^\ast\), may exist as a solution to \(D_\text{db}(x^\ast)=0\). If \(x^\ast\) exists and is convergence stable then it is also evolutionarily stable because the two stability conditions are identical ([[spatial adaptive dynamics#Selection gradient, convergent and evolutionary stability|the mixed derivatives are zero]]). In particular, cooperation can be maintained in spatially structured populations, a result that is of course in line with classical theory. More specifically, cooperative investments can increase if the marginal benefits, \(B^\prime(x)\), exceed the \(k\)-fold marginal costs, \(C^\prime(x)\), which is reminiscent of the \(b>ck\)-rule in the traditional donation game (see [[Spatial social dilemmas promote diversity#References|Ohtsuki et al. 2006]]). | |||
=== Linear costs and benefits === | |||
The evolutionary analysis becomes particularly simple for linear benefit and cost functions \(B(x)=x\) and \(C(x)=r x\), where \(r\) denotes the (marginal) cost-to-benefit ratio. Again, population structures are capable of supporting cooperation for sufficiently small \(r\). More precisely, the selection gradient \(D_\text{db}(x)=w\frac{k-2}{k(k-1)}(1-k r)\) is reduced to a constant (c.f. Eq. \eqref{eq:d:pd:dB}), and hence no singular strategy exists. However, the gradient changes sign for \(r^\ast=1/k\). Thus, for favourable cost-to-benefit ratios, \(r<r^\ast\), investments increase to their maximum, whereas for harsher conditions, \(r>r^\ast\) cooperative investments cannot be sustained, see Fig. 1. | |||
[[Image:Diversification - linear continuous PD (equilibria).jpg|550px]] | |||
'''Figure 1:''' Equilibrium investment levels (mean \(\pm\) standard deviation) in individual-based simulations of the linear continuous prisoner's dilemma (\(B(x)=x, C(x)=r x\)) as a function of the cost-to-benefit ratio, \(r\), for weak selection, \(w=1\) (red), moderate, \(w=10\) (black), and strong selection, \(w=100\) (blue). | |||
''A'' in well-mixed populations with \(N=10^4\) individuals cooperative investments are close to zero regardless of \(r\) as predicted by adaptive dynamics (dashed line). The small variance further decreases for stronger selection emphasizing the disadvantage of mutants with higher investments. | |||
''B'' for populations with \(k=4\) neighbours spatial adaptive dynamics predicts a threshold \(r^\ast=1/k\) (dash-dotted-line) below which investments reach the maximum but disappear above. Simulations on a \(100\times 100\) lattice confirm the trend but reveal an interesting susceptibility to noise: for weak selection (red) the maximum investment is not reached; intermediate selection (black) essentially follows pair approximation, while strong selection (blue) maintains non-zero investment levels beyond the predicted threshold. The large variation suggests co-existence of different traits and is confirmed through sample snapshots of the spatial configuration in Fig. 2i. | |||
====Interactive labs, Figure 1 A==== | |||
{| class=wikitable align=center | |||
|+ | |||
| colspan="4" | | |||
Dynamics in well-mixed populations with size \(N=10^4\) for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as weak, moderate or strong selection, \(w=1, 10, 100\). | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! well-mixed !!\(w=1\)!!\(w=10\)!!\(w=100\) | |||
|- | |||
! \(r=0.1\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,1 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,10 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,100 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! \(r=0.3\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,1 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,10 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,100 --geometry M --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
|} | |||
====Interactive labs, Figure 1 B==== | |||
{| class=wikitable align=center | |||
|+ | |||
| colspan="4" | | |||
Dynamics in on \(N=100\times100\) square lattices with \(k=4\) neighbours for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as weak, moderate or strong selection, \(w=1, 10, 100\). | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! lattice, \(k=4\) !!\(w=1\)!!\(w=10\)!!\(w=100\) | |||
|- | |||
! \(r=0.1\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,1 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,10 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,100 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! \(r=0.3\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,1 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,10 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,100 --geometry m --init gaussian 0.5,0.01 --interactions r1 --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
|} | |||
Interestingly, these analytical predictions are not always borne out in individual-based models when the selection strength, \(w\), is large. The reasons for the differences can be appreciated by looking at pairwise invasibility plots (\(PIP\)), which show the regions in \((x,y)\)-space in which a mutant \(y\) can invade a resident \(x\), i.e., regions for which the invasion fitness \(f(x,y)\) is positive. To construct these plots, we first solve the dynamical equation \(\dot q_{m|m}=0\) (see [[spatial adaptive dynamics]]) to find the equilibrium \(q^\ast_{m|m}\) for given resident and mutant trait values \(x, y\) and then determine the sign of the corresponding invasion fitness. An example is shown in Fig. 2g with \(r>1/k\) so that adaptive dynamics predicts evolution to pure defection. | |||
[[Image:Diversification - linear continuous PD (dynamics).jpg|825px]] | |||
'''Figure 2:''' Linear continuous prisoner's dilemma in \(100\times 100\) lattice populations with \(k=4\) neighbours. Evolutionary dynamics is illustrated for favourable cost-to-benefit ratios, \(r=0.1<1/k\) (A-C), and for harsher conditions, \(r=0.3>1/k\), with moderate selection, \(w=10\) (D-F) as well as strong selection, \(w=100\) (G–I). | |||
The left column shows the pairwise invasibility plots (\(PIP\)), which indicate whether mutant traits are capable of invading a particular resident population (white regions) or not (black regions). | |||
The middle column shows the evolutionary trajectory of the distribution of investments over time in individual-based simulations (darker shades indicate higher trait densities in the population with the highest densities in yellow). | |||
The right column depicts snapshots of the population configuration at the end of the simulation runs. The colour hue indicates the investment levels ranging from low (red) to intermediate (green) and high (blue). | |||
For \(r<1/k\) higher investors can always invade and eventually the maximum investment is reached (A–C), regardless of selection strength. | |||
The situation is reversed for \(r>1/k\) and weak to moderate selection where only lower investors can invade and investments dwindle to zero (D–F). | |||
Interestingly, for strong selection in lattice populations not only lower investors can invade for \(r>1/k\) but also those that invest significantly more than the resident (G–I). Note that the width of the region of unfavourable mutants decreases with increasing selection strength \(w\), i.e. the gap becomes easier to bridge (but does not depend on the resident trait \(x\); grey area for \(w=50\) and black area for \(w=100\)). Nevertheless adaptive dynamics predicts that investments evolve to zero because of the assumption that mutations are small, which restrict the dynamics to the diagonal of the \(PIP\). However, individual-based simulations show that rare larger mutations or a sequence of smaller ones can give rise to the co-existence of high and low investors. The outcome does not depend on the initial configuration of the population. | |||
====Interactive labs, Figure 2==== | |||
{| class=wikitable align=center | |||
|colspan="3"| | |||
Dynamics on a square \(100\times100\) lattice with \(k=4\) neighbours for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as moderate or strong selection, \(w=10, 100\). | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! '''A-C:''' \(r=0.1\), \(w=10\) !! '''D-F:''' \(r=0.3\), \(w=10\) !! '''G-I:''' \(r=0.3\), \(w=100\) | |||
|- | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.1 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 0 1 --costs 0 0.3 --delay 100 --fitnessmap exp 1,100 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|} | |||
For mutants \(y\) sufficiently close to the resident \(x\), \(f(x,y)>0\) only holds for \(y<x\), so that evolution by (infinitesimally) small mutations, as envisaged in adaptive dynamics, indeed leads to ever smaller investment. However, the \(PIP\) also shows positive invasion fitness for mutants \(y>x\) if \(y\) is sufficiently larger than \(x\) (white area above the diagonal in Fig. 2g). In individual-based models, mutations are normally distributed around the parental trait and of finite size such that stochastically appearing larger mutations or sequences of smaller mutations in the right direction can give rise to the co-existence of high and low investors (see Fig. 2i). Thus, evolutionary diversification is possible in individual-based models despite the absence of evolutionary branching points in the adaptive dynamics, and even if the analytical prediction is evolution of pure defection. Note that this mode of evolutionary diversification is a feature of spatial structure that does not occur in the corresponding well-mixed models. | |||
=== Saturating benefits === | === Saturating benefits === | ||
The continuous prisoner's dilemma was first introduced in [[#References|Killingback et al. 1999]] with saturating benefits \(B(x)=b_0\left( \exp{(-b_1 x)} \right)\) and linear costs \(C(x)=c_0 x\) (\(b_0, b_1, c_0>0\)). Using individual-based simulations these authors showed that structured populations are capable of supporting cooperation, whereas well-mixed populations are not. Spatial adaptive dynamics provides an analytical perspective on these results. For the given cost and benefit functions, we have: | |||
\begin{align} | |||
\label{eq:d:kdk:dB} | |||
D_\text{db}(x) &= w\frac{k-2}{k(k-1)}\left( b_0 b_1 e^{-b_1 x}-c_0 k\right)\\ | |||
\label{eq:cssess:kdk:dB} | |||
CS_\text{db}(x^\ast) &= ES_\text{db}(x^\ast) = -w\frac{k-2}{k-1}b_1 c_0<0. | |||
\end{align} | |||
There is a singular point at | |||
\begin{align} | |||
\label{eq:d:kdk:xast} | |||
x^\ast &= \frac1{b_1}\log\left(\frac{b_0 b_1}{c_0 k}\right). | |||
\end{align} | |||
The singular point is always convergence stable as well as evolutionarily stable (see Fig. 3b). | |||
[[Image:Diversification - continuous PD, saturating benefits (dynamics).jpg|825px]] | |||
'''Figure 3:''' Continuous prisoner's dilemma with saturating benefits \(B(x)=b_0\left(1-\exp{(-b_1 x)}\right)\) and linear costs \(C(x)=c_0 x\) for \(b_0=8, b_1=1, c_0=0.7\) in \(100\times 100\) lattice populations for weak selection, \(w=1\) (top row) | |||
and strong selection, \(w=100\) (bottom row). | |||
The pairwise invasibility plots (\(PIP\), left column) show that higher investing mutants can invade for low resident investments and lower investing mutants can invade high investing residents. However, near the singular investment level, \(x^\ast=\log\left(\frac{b_0 b_1}{k c_0}\right)/b_1\approx1.050\), selection strength gives rise to interesting differences in the dynamics. | |||
''A'' for weaker selection, \(w=1\), \(x^\ast\) is evolutionarily stable. This is confirmed through individual-based simulations. | |||
''B'' depicts the investment distribution over time (darker shades indicate higher trait densities in the population with the highest densities in yellow). | |||
''C'' shows a snapshot of the spatial configuration at the end of the simulation. The colour hue indicates the investment level ranging from low (red) to intermediate (green) to high (blue). In contrast, ''D'' for strong selection, \(w=100\), \(x^\ast\) can be invaded but only by higher investing mutants. As a consequence, a degenerate form of evolutionary branching may occur. Individual-based simulations confirm branching already for \(w=10\) (''E'', ''F''). | |||
====Interactive labs, Figure 3==== | |||
{| class=wikitable align=center | |||
|colspan="2"| | |||
Dynamics on a square \(100\times100\) lattice with \(k=4\) neighbours for saturating benefits, \(B(x)=b_0\left(1-\exp{(-b_1 x)}\right)\) and linear costs \(C(x)=c_0 x\) for \(b_0=8, b_1=1, c_0=0.7\) with \(b_0=8, b_1=1, c_0=0.7\) with weak, \(w=1\) and stronger \(w=10\) selection. | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! '''A-C:''' weak selection \(w=1\) !! '''D-F:''' stronger selection \(w=10\) | |||
|- | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 4 8,1 --costs 0 0.7 --delay 100 --fitnessmap exp 1,1 --geometry n --init gaussian 0.2,0.02 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,2 --view Traits_-_Distribution"}} | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 4 8,1 --costs 0 0.7 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.2,0.02 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,2 --view Traits_-_Distribution"}} | |||
|} | |||
Interestingly, the adaptive dynamics analysis again misses subtle but intriguing effects arising from strong selection. A pairwise invasibility plot for strong selection is shown in Fig. 3D) and reveals that \(x^\ast\) is susceptible to invasion by mutants with slightly higher investments. In individual-based models, this effectively turns \(x^\ast\) into a (degenerate) branching point, i.e., a starting point for evolutionary diversification. The diversification into coexisting high and low investors has already been observed in [[#References|Killingback et al. 1999]], but the underlying mechanism had not been addressed. The earlier results were based on a different, deterministic update rule, according to which a focal individual imitated the strategy of the best performing neighbour, including itself, but this update rule essentially corresponds to death-birth updating with very strong selection (the only difference being that the focal individual is removed). Hence the diversification reported in [[#References|Killingback et al. 1999]] is of the same type as the one seen here for strong selection. | |||
== Evolution in the continuous snowdrift game == | == Evolution in the continuous snowdrift game == | ||
In the continuous snowdrift game the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x+y)-C(y)\). Note that this generalization to continuous strategies does not imply that every interaction between an individual with strategy \(x\) and another with strategy \(y\) invariably results in a snowdrift game. In fact, snowdrift games in this narrower sense appear only if the two traits \(x, y\) straddle the singular strategy \(x^\ast\). Depending on the cost and benefit functions, as well as on the strategies \(x\) and \(y\), any kind of \(2\times2\) game can arise, including a prisoner's dilemma, in which the lower investing strategy dominates ([[Spatial social dilemmas promote diversity#References|Doebeli et al. 2004]], [[Spatial social dilemmas promote diversity#References|Doebeli et al. 2013]]). In this sense the framework of the continuous snowdrift game actually encompasses the gist of the continuous prisoner's dilemma for sufficiently high costs -- just as the classical snowdrift game turns into a prisoner's dilemma (see [[Spatial social dilemmas promote diversity#References|Hauert & Doebeli, 2004]]). | In the continuous snowdrift game the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x+y)-C(y)\). Note that this generalization to continuous strategies does not imply that every interaction between an individual with strategy \(x\) and another with strategy \(y\) invariably results in a snowdrift game. In fact, snowdrift games in this narrower sense appear only if the two traits \(x, y\) straddle the singular strategy \(x^\ast\). Depending on the cost and benefit functions, as well as on the strategies \(x\) and \(y\), any kind of \(2\times2\) game can arise, including a prisoner's dilemma, in which the lower investing strategy dominates ([[Spatial social dilemmas promote diversity#References|Doebeli et al. 2004]], [[Spatial social dilemmas promote diversity#References|Doebeli et al. 2013]]). In this sense the framework of the continuous snowdrift game actually encompasses the gist of the continuous prisoner's dilemma for sufficiently high costs -- just as the classical snowdrift game turns into a prisoner's dilemma (see [[Spatial social dilemmas promote diversity#References|Hauert & Doebeli, 2004]]). | ||
Following [[spatial adaptive dynamics]], the selection gradient for the continuous snowdrift game in structured populations with death-birth updating is given by | |||
\begin{align} | \begin{align} | ||
\label{eq:d:csd:dB} | \label{eq:d:csd:dB} | ||
| Line 60: | Line 195: | ||
x^\ast_\text{db} &= \frac{b_1(k+1)-c_1 k}{2c_2k-4b_2(k+1)}. | x^\ast_\text{db} &= \frac{b_1(k+1)-c_1 k}{2c_2k-4b_2(k+1)}. | ||
\end{align} | \end{align} | ||
The numerator of \eq | The numerator of Eq. \eqref{eq:xs:csd:dB} is positive if and only if the condition for evolution away from zero, \(b_1>\frac{k}{k+1}c_1\), is satisfied. Similarly, the denominator of Eq. \eqref{eq:xs:csd:dB} is positive if and only if \(2b_2(k+1)<c_2k\) (recall \(b_2, c_2<0\)). It is clear from Eq. \eqref{eq:css:csd:dB} that this is also the condition for convergence stability. Thus, if a singular point, \(x^\ast\), exists, cooperative traits either evolve away from zero and \(x^\ast\) is convergence stable, or the trait cannot evolve away from zero and \(x^\ast\) is a repellor. | ||
We note that if the singular point exists, \(x^\ast\), it is shifted towards smaller investments for a given set of parameters, as compared to well-mixed populations with the same parameters: \(x^\ast = \frac{b_1-c_1}{2c_2-4b_2}\). Furthermore, the condition for convergence stability, \(2b_2(k+1)<c_2k\), is less restrictive than the corresponding condition \(2b_2<c_2\) in the well-mixed case. Finally, from \eq{ess:csd:dB} we see that the condition for evolutionary stability is \(b_2(k+2)(k+1)<c_2 k^2\), which is again less restrictive than the corresponding condition \(b_2<c_2\) in the well-mixed case. Combining the two stability conditions shows that evolutionary branching occurs for \(2b_2(k+1)/k<c_2<b_2(k+1)(k+2)/k^2\). Thus, the analytical approach based on pair approximation suggests that population structures tend to inhibit evolutionary diversification by decreasing the range of parameters for which the singular point is an evolutionary branching point (c.f. Fig. 4A & C). | |||
[[Image:Diversification - continuous SD (dB equilibria).jpg|825px]] | |||
'''Figure 4:''' Continuous snowdrift game with quadratic benefit and cost functions, \(B(x)=b_1 x+b_2 x^2\) and \(C(x)=c_1 x+c_2 x^2\). Evolutionary outcomes are shown as a function of the benefit parameter \(b_1\) and cost parameter \(c_2\) with \(b_2=-1/4\) and \(c_1 = 2\). Note that \(b_1<2\) violates the assumption \(B(x)>C(x)\) at least for small \(x\) and hence effectively mimics the characteristics of the prisoner's dilemma. | |||
<strong>A</strong> analytical predictions based on adaptive dynamics in well-mixed populations and | |||
<strong>B</strong> results from individual-based simulations for populations with \(N=10^4\) individuals. | |||
<strong>C</strong> analytical predictions based on spatial adaptive dynamics and complementing individual-based simulations on \(100\times 100\) lattices for | |||
<strong>D</strong> moderate selection, \(w=10\), and | |||
<strong>E</strong> strong selection, \(w=100\). | |||
In lattice populations the parameter region admitting singular strategies is shifted to both smaller values of \(b_1\) and of \(c_2\) and the size of the region admitting evolutionary branching is markedly smaller than in well-mixed populations (< strong>A, C</strong>). | |||
Interestingly, spatial adaptive dynamics predicts branching only for parameters where defection dominates in well-mixed populations, \(b_1<c_1\), mimicking the continuous prisoner's dilemma. For weak to moderate selection predictions by adaptive dynamics (<strong>A, C</strong>) are in good agreement with results from individual-based simulations (<strong>B, D</strong>), where equilibrium investment levels range from the minimum (black) to intermediate (grey) and the maximum (white) augmented by convergence stability (red) and evolutionary instability (blue) with the overlapping region indicating evolutionary branching (maroon) in adaptive dynamics and diversification in simulations. | |||
For strong selection (<strong>E</strong>) striking differences arise with a much increased region of diversification. The points labelled <strong>a-d</strong> indicate the parameter settings for the invasion analysis in Fig. 5. Note that the automated classification of investment distributions becomes more difficult whenever the singular investment \(x^\ast\) is close to zero or one. | |||
The results for well-mixed populations summarized in Fig. 4A & B can be replicated and verified in the tutorial [[Origin of Cooperators and Defectors]]. The following labs illustrate the dynamical regimes in spatially structured populations. | |||
====Interactive labs, Figure 4==== | |||
{| class=wikitable align=center | |||
|+ | |||
| colspan="2" | | |||
Dynamical regimes in the spatial continuous snowdrift game for moderate selection, \(w=10\), on \(N=100\times100\) square lattices with \(k=4\) neighbours. | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! branching, \(c_2=-0.5,b_1=1.65\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.65,-0.25 --costs 1 2,-0.5 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! attractor, \(c_2=-0.3,b_1=1.9\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.9,-0.25 --costs 1 2,-0.3 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! repellor, \(c_2=-0.75,b_1=1.5\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.5,-0.25 --costs 1 2,-0.75 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! zero investments, \(c_2=-0.5,b_1=1.5\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.5,-0.25 --costs 1 2,-0.5 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! full investments, \(c_2=-0.5,b_1=2\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 2,-0.25 --costs 1 2,-0.5 --delay 100 --fitnessmap exp 1,10 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
|} | |||
Strong selection greatly enhance the parameter region resulting in a diversity of traits, see Fig. 4E. The parameter combinations marked with points <strong>a,b,c,d</strong> refer to modes of diversification that do not rely on evolutionary branching and only occur in spatially structured populations. | |||
[[Image:Diversification - continuous SD (dB modes).jpg|825px]] | |||
'''Figure 5:''' Spatial modes of diversification in the continuous snowdrift game with quadratic benefit and cost functions. | |||
<strong>A-D</strong> depict pairwise invasibility plots (<em>PIP</em>, top row) for the four scenarios illustrating increased spatial diversification due to strong selection (c.f. parameter combinations <strong>a-d</strong> marked in Fig. 4). In all cases the width of the region of disadvantageous mutants decreases with selection strength (grey for \(w=1\); black for \(w=100\)). | |||
<strong>A</strong> the <em>PIP</em> suggests gradual evolution towards minimal investments, except for smaller resident traits, where not only lower investing mutants can invade but also those making markedly higher investing. | |||
<strong>B</strong> higher investing mutants can always invade, but so can traits investing markedly less. | |||
<strong>C</strong> selection strength distorts the <em>PIP</em> in the vicinity of the convergence and evolutionarily stable \(x^\ast\) resulting in a degenerate form of branching (c.f. Fig. 3). | |||
<strong>D</strong> the <em>PIP</em> indicates that \(x^\ast\) is a repellor such that residents with \(x<x^\ast\) are invaded by lower investors while those with \(x>x^\ast\) by higher investors. However, as a consequence of strong selection, mutants with markedly higher (lower) investments can also invade. | |||
<strong>E-H</strong> depict corresponding plots of regions of mutual invasibility (<em>PIP\(^\text{2}\)</em>, white regions). Regions where mutants or residents are unable to invade (grey) are marked with \((+,-)\) and \((-,+)\), respectively. The vector field shows the [[Spatial adaptive dynamics#Evolutionary divergence of coexisting traits|evolutionary divergence]] and indicates the direction of selection for two co-existing residents based on analytical approximations of the spatial invasion dynamics. In all cases divergence drives the traits away from the diagonal and hence preserves diversity.<br> | |||
<em>Parameters:</em> \(b_2=-1/4, c_1=2\), <strong>A</strong> \(b_1=1.55\), \(c_2=-0.6\); <strong>B</strong> \(b_1=1.65\), \(c_2=-0.625\); <strong>C</strong> \(b_1=1.9\), \(c_2=-0.3\); <strong>D</strong> \(b_1=1.5\), \(c_2=-0.72\). | |||
====Interactive labs, Figure 5==== | |||
{| class=wikitable align=center | |||
|+ | |||
| colspan="2" | | |||
Modes of diversification in the spatial continuous snowdrift game. The parameter settings refer to points <strong>a,b,c,d</strong> in Fig. 4E. | |||
The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to: | |||
{{Legend:Gradient|label=Densities|min=Low|max=High|gradient=white,black,yellow,red}} | |||
|- | |||
! Figure 5A & E, Figure 4E a, \(c_2=-0.6,b_1=1.55\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.55,-0.25 --costs 1 2,-0.6 --delay 100 --fitnessmap exp 1,100 --geometry n --init gaussian 0.9,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! Figure 5B & F, Figure 4E b, \(c_2=-0.625,b_1=1.65\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.65,-0.25 --costs 1 2,-0.625 --delay 100 --fitnessmap exp 1,100 --geometry n --init gaussian 0.2,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! Figure 5C & G, Figure 4E c, \(c_2=-0.3,b_1=1.9\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.9,-0.25 --costs 1 2,-0.3 --delay 100 --fitnessmap exp 1,100 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
! Figure 5D & H, Figure 4E d, \(c_2=-0.72,b_1=1.5\) | |||
|{{EvoLudoTrigger| | |||
options="--module cSD --benefits 11 1.5,-0.25 --costs 1 2,-0.72 --delay 100 --fitnessmap exp 1,100 --geometry n --init gaussian 0.1,0.01 --interactions all --mutation 0.01 gaussian 0.01 --popsize 100x --popupdate d --timestep 20 --traitrange 0,1 --view Traits_-_Distribution"}} | |||
|- | |||
|} | |||
== Conclusions & Discussion == | == Conclusions & Discussion == | ||
| Line 69: | Line 287: | ||
Structured populations offer new modes of diversification that are driven by an interplay of finite-size mutations and population structures. Trait variation is more easily maintained in structured populations due to the slower spreading of advantageous traits as compared to well-mixed populations. Spatial adaptive dynamics is unable to capture these new modes of diversification because of the underlying assumption that the resident population is composed of discrete traits (monomorphic before branching and dimorphic or polymorphic after branching). Nevertheless, invasion analysis and pairwise invasibility plots, \(PIP\), in particular, provide an intuitive interpretation for additional pathways to diversification that are introduced by spatial structures and further promoted for increasing selection strength. Even in the vicinity of evolutionarily stable investments, trait combinations exist that admit mutual invasion and hence can coexist. However, such states cannot evolve through adaptive dynamics but are nevertheless accessible to trait distributions around the evolutionarily stable trait and can drive a degenerate form of branching. Moreover, spatial invasion fitness can open up new regions in trait space for mutant invasion. However, those regions need not be accessible by small mutational steps, and instead require stochastically appearing larger mutations or sequences of smaller mutations that allow to bridge regions of unfavourable traits. | Structured populations offer new modes of diversification that are driven by an interplay of finite-size mutations and population structures. Trait variation is more easily maintained in structured populations due to the slower spreading of advantageous traits as compared to well-mixed populations. Spatial adaptive dynamics is unable to capture these new modes of diversification because of the underlying assumption that the resident population is composed of discrete traits (monomorphic before branching and dimorphic or polymorphic after branching). Nevertheless, invasion analysis and pairwise invasibility plots, \(PIP\), in particular, provide an intuitive interpretation for additional pathways to diversification that are introduced by spatial structures and further promoted for increasing selection strength. Even in the vicinity of evolutionarily stable investments, trait combinations exist that admit mutual invasion and hence can coexist. However, such states cannot evolve through adaptive dynamics but are nevertheless accessible to trait distributions around the evolutionarily stable trait and can drive a degenerate form of branching. Moreover, spatial invasion fitness can open up new regions in trait space for mutant invasion. However, those regions need not be accessible by small mutational steps, and instead require stochastically appearing larger mutations or sequences of smaller mutations that allow to bridge regions of unfavourable traits. | ||
Previous attempts at amalgamating adaptive dynamics and spatial structure have not observed spontaneous diversification or evolutionary branching. In particular, [[Spatial social dilemmas promote diversity#References|Allen et al. (2013)]] augment adaptive dynamics by structure coefficients ([[Spatial social dilemmas promote diversity#References|Tarnita et al. 2011]]), which restrict the analysis to weak selection. Moreover, their framework is fundamentally different from ours because it is based on fixation probabilities rather than invasion fitness. More specifically, their analysis is based on the fixation probabilities \(p_x\) and \(p_y\) of two types \(x\) and \(y\) in a population consisting of \(x\) and \(y\): \(x\) is favoured over \(y\) if \(p_x>p_y\) (see Eq. | Previous attempts at amalgamating adaptive dynamics and spatial structure have not observed spontaneous diversification or evolutionary branching. In particular, [[Spatial social dilemmas promote diversity#References|Allen et al. (2013)]] augment adaptive dynamics by structure coefficients ([[Spatial social dilemmas promote diversity#References|Tarnita et al. 2011]]), which restrict the analysis to weak selection. Moreover, their framework is fundamentally different from ours because it is based on fixation probabilities rather than invasion fitness. More specifically, their analysis is based on the fixation probabilities \(p_x\) and \(p_y\) of two types \(x\) and \(y\) in a population consisting of \(x\) and \(y\): \(x\) is favoured over \(y\) if \(p_x>p_y\) (see Eq. 4 and formulas following Eq. 7 in [[Spatial social dilemmas promote diversity#References|Allen et al. 2013]]). Clearly, it is then impossible to have both types be favoured in an \((x,y)\)-population, but this is exactly the requirement for mutual coexistence. In fact, Allen et al. acknowledge that fixation probabilities are "less appropriate" for studying evolutionary branching and that instead "establishment probabilities" should be considered for studying diversification. As a consequence their adaptive dynamics derivation precludes its most intriguing feature, that of evolutionary branching. However, in the limit of weak selection the two approaches are compatible in some aspects. For example, the selection gradient and the condition for convergence stability reported for the continuous prisoner's dilemma are identical (c.f. Eqs. \eqref{eq:d:csd:dB}, \eqref{eq:css:csd:dB} and their Eqs. (11), (13)). In our framework, the use of invasion fitness allows to determine evolutionary stability, and the corresponding \(PIP\)'s reveal the potential for degenerate forms of branching – but only for stronger selection (see Fig. 3). Another attempt at spatial adaptive dynamics considers spatial structure in the form of demes ([[Spatial social dilemmas promote diversity#References|Parvinen et al. 2017]]). However, quite naturally such deme structures suppress branching because in the long run it is impossible to maintain multiple co-existing traits in small demes, which quickly become homogeneous. Instead, branching is only possible if demes are large enough to support branching in every single one. | ||
Interestingly, in well-mixed populations evolutionary branching is only observed for the continuous snowdrift game, where two distinct traits of high and low investors can co-exist and essentially engage in a classical (discrete) snowdrift game. In contrast, in structured populations with death-birth updating, evolutionary branching is only observed for prisoner's dilemma type interactions where lower investments invariably dominate higher ones, which applies both in the continuous prisoner's dilemma as well as the continuous snowdrift game with sufficiently high costs. The reason for this surprising difference can be understood intuitively by considering the preferred spatial configurations in the two classical (discrete) games: in the prisoner's dilemma cooperators form compact clusters to reduce exploitation by defectors (minimize surface), while in the snowdrift game filament like clusters form because it is advantageous to adopt a strategy that is different from that of the interaction partners (maximize surface). In the continuous variants of those games it is naturally much harder to maintain and spread distinct traits in fragmented filament-like structures because they are more prone to effects of noise than compact clusters. Effectively this fragmentation inhibits evolutionary branching because diverging traits tend to trigger further fragmentation and as a consequence do not survive long enough to get established and form their own branch. In contrast, the compact clusters promoted by the prisoner's dilemma provide structural protection for higher investors and thus help drive diversification. | Interestingly, in well-mixed populations evolutionary branching is only observed for the continuous snowdrift game, where two distinct traits of high and low investors can co-exist and essentially engage in a classical (discrete) snowdrift game. In contrast, in structured populations with death-birth updating, evolutionary branching is only observed for prisoner's dilemma type interactions where lower investments invariably dominate higher ones, which applies both in the continuous prisoner's dilemma as well as the continuous snowdrift game with sufficiently high costs. The reason for this surprising difference can be understood intuitively by considering the preferred spatial configurations in the two classical (discrete) games: in the prisoner's dilemma cooperators form compact clusters to reduce exploitation by defectors (minimize surface), while in the snowdrift game filament like clusters form because it is advantageous to adopt a strategy that is different from that of the interaction partners (maximize surface). In the continuous variants of those games it is naturally much harder to maintain and spread distinct traits in fragmented filament-like structures because they are more prone to effects of noise than compact clusters. Effectively this fragmentation inhibits evolutionary branching because diverging traits tend to trigger further fragmentation and as a consequence do not survive long enough to get established and form their own branch. In contrast, the compact clusters promoted by the prisoner's dilemma provide structural protection for higher investors and thus help drive diversification. | ||
| Line 85: | Line 303: | ||
# Doebeli M, Hauert C, Killingback T (2013) A comment on "Towards a rigorous framework for studying 2-player continuous games" by Shade T. Shutters, Journal of Theoretical Biology 321, 40--43, 2013. ''J. Theor. Biol.'' '''336''' 240–241. | # Doebeli M, Hauert C, Killingback T (2013) A comment on "Towards a rigorous framework for studying 2-player continuous games" by Shade T. Shutters, Journal of Theoretical Biology 321, 40--43, 2013. ''J. Theor. Biol.'' '''336''' 240–241. | ||
# Hauert C, Doebeli M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. ''Nature'' '''428''' 643–646. | # Hauert C, Doebeli M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. ''Nature'' '''428''' 643–646. | ||
# Killingback, T., Doebeli, M., & Knowlton, N. (1999) Variable investment, the continuous prisoner's dilemma, and the origin of cooperation. ''Proc. R. Soc. B'' '''266''' 1723–1728. | |||
# Ohtsuki, H., Hauert, C., Lieberman, E., & Nowak, M.A. (2006) A simple rule for the evolution of cooperation on graphs. ''Nature'' '''441''' 502–505. | # Ohtsuki, H., Hauert, C., Lieberman, E., & Nowak, M.A. (2006) A simple rule for the evolution of cooperation on graphs. ''Nature'' '''441''' 502–505. | ||
# Parvinen, K., Ohtsuki, H., & Wakano, J.Y. (2017) The effect of fecundity derivatives on the condition of evolutionary branching in spatial models. ''J. Theor. Biol.'' '''416''' | # Parvinen, K., Ohtsuki, H., & Wakano, J.Y. (2017) The effect of fecundity derivatives on the condition of evolutionary branching in spatial models. ''J. Theor. Biol.'' '''416''' 129–143. | ||
# Tarnita, C.E., Wage, N., & Nowak, M.A. (2011) Multiple strategies in structured populations. ''Proc. Natl. Acad. Sci. USA'' '''108''' 2334–2337. | # Tarnita, C.E., Wage, N., & Nowak, M.A. (2011) Multiple strategies in structured populations. ''Proc. Natl. Acad. Sci. USA'' '''108''' 2334–2337. | ||
Latest revision as of 01:27, 19 February 2026
Cooperative investments in social dilemmas can spontaneously diversify into stably co-existing high and low contributors in well-mixed populations. Here we extend the analysis to emerging diversity in (spatially) structured populations. Using pair approximation we derive analytical expressions for the invasion fitness of rare mutants in structured populations, which then yields a spatial adaptive dynamics framework. This allows us to predict changes arising from population structures in terms of existence and location of singular strategies, as well as their convergence and evolutionary stability as compared to well-mixed populations. Based on spatial adaptive dynamics and extensive individual based simulations, we find that spatial structure has significant and varied impacts on evolutionary diversification in continuous social dilemmas. More specifically, spatial adaptive dynamics suggests that spontaneous diversification through evolutionary branching is suppressed, but simulations show that spatial dimensions offer new modes of diversification that are driven by an interplay of finite-size mutations and population structures. Even though spatial adaptive dynamics is unable to capture these new modes, they can still be understood based on an invasion analysis. In particular, population structures alter invasion fitness and can open up new regions in trait space where mutants can invade, but that may not be accessible to small mutational steps. Instead, stochastically appearing larger mutations or sequences of smaller mutations in a particular direction are required to bridge regions of unfavourable traits. The net effect is that spatial structure tends to promote diversification, especially when selection is strong.
Social dilemmas with continuous traits
Social dilemmas are important mathematical metaphors for studying the problem of cooperation. The best studied models of social dilemmas are the prisoner's dilemma and the snowdrift game. Traditionally, such models are often restricted to the two distinct strategies of cooperate, \(C\), and defect, \(D\). However, these models can easily be extended to describe a continuous range of cooperative investments into a public good. In such continuous games, the aim is to study the evolutionary dynamics of the level of investment.
For example, in the donation game, which is the most prominent version of the prisoner's dilemma, cooperators confer a benefit \(b\) to their interaction partners at a cost \(c\) to themselves. Defection entails neither costs nor confers benefits. With \(b>c>0\), both individuals prefer mutual cooperation, which pays \(b-c\), over a zero payoff for mutual defection. However, the temptation to shirk costs and free ride on benefits provided by the partner undermines cooperation to the detriment of all. In fact, defection is the dominant strategy because it results in higher payoffs regardless of the partner's strategy. This conflict of interest between the individual and the group represents the hallmark of social dilemmas.
Continuous Donation game
A natural translation of the donation game to continuous traits is based on cost and benefit functions, \(C(x)\) and \(B(x)\), where the trait \(x\in[0,x_\text{max}]\) represents a level of cooperative investment that can vary continuously. In the spirit of the donation game, an individual with strategy \(x\) interacting with an \(y\)-strategist obtains a payoff \(P(x,y)=B(y)-C(x)\). Assuming that
- zero investments incur no costs and provide no benefits, \(B(0)=C(0)=0\),
- benefits exceed costs, \(B(x)>C(x)\geq0\), and
- are increasing functions, \(B^\prime(x), C^\prime(x)\geq0\),
recovers the social dilemma of the donation game for continuous investment levels: the level of investment invariably evolves to zero, which corresponds to pure defection, despite the fact that both players would be better off at non-zero investment levels. The reason is that an actor can only influence the cost \(C(x)\) of an interaction, but not the received benefit \(B(y)\), and hence selection can only act to minimize costs.
Continuous Snowdrift game
In a weaker form of a social dilemma, the snowdrift game, cooperators also provide benefits, \(b\), at a cost, \(c\). However, benefits are now accessible to both individuals and accumulate in a discounted manner. For example, yeast secretes enzymes for extra cellular digestion of sucrose. While access to nutrients is crucial, the marginal value of additional resources diminishes and may exceed the intake capacity. As a result, the social dilemma remains in effect, because the most favourable outcome of mutual cooperation remains prone to cheating, but the dilemma is relaxed because it pays to cooperate against defectors. Again, it is straightforward to formulate a continuous version of the snowdrift game. In contrast to the donation game, in the continuous snowdrift game the benefits depend on the strategies of both interacting individuals. For example, for simplicity one can assume that benefits depend on the aggregate investment levels of both players, so that the benefit is a function \(B(x+y)\). Assuming a cost function \(C(x)\), an \(x\) strategist interacting with strategy \(y\) obtains a payoff \(P(x,y)=B(x+y)-C(x)\), again with \(B(0)=C(0)=0\), \(B(x)>C(x)\geq0\) and \(B^\prime(x),C^\prime(x)\geq0\), as before, but with the additional constraint \(C(x)>B(x+y)-B(y)\) for sufficiently large \(y\) so that the increased return from investments of an individual do not outweigh its costs when interacting with high investors. Typically this is achieved by saturating benefit functions, \(B^{\prime\prime}(x)<0\).
The gradual evolution of continuous traits can be described using the framework of adaptive dynamics. Below we extend this framework to spatial settings by amalgamating adaptive dynamics and pair approximation into spatial adaptive dynamics. This provides the toolbox to investigate the impact of spatial structures on the evolution of cooperation in the prisoner's dilemma as well as the snowdrift games.
Evolution in the continuous prisoner's dilemma
In the continuous prisoner's dilemma the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x)-C(y)\). This implies that the selection gradient in well-mixed populations is proportional to \(-C'(x)\), and hence, assuming monotonously increasing costs, no singular strategy exists apart from the pure defection state \(x=0\), and the population always evolves to that state, regardless of how large the benefits of cooperation are. In contrast, for death-birth updating in structured populations the selection gradient for spatial adaptive dynamics becomes \begin{align} \label{eq:d:pd:dB} D_\text{db}(x) &= w\frac{k-2}{k(k-1)}(B^\prime(x)-k C^\prime(x)). \end{align} Thus, in structured populations a singular strategy, \(x^\ast\), may exist as a solution to \(D_\text{db}(x^\ast)=0\). If \(x^\ast\) exists and is convergence stable then it is also evolutionarily stable because the two stability conditions are identical (the mixed derivatives are zero). In particular, cooperation can be maintained in spatially structured populations, a result that is of course in line with classical theory. More specifically, cooperative investments can increase if the marginal benefits, \(B^\prime(x)\), exceed the \(k\)-fold marginal costs, \(C^\prime(x)\), which is reminiscent of the \(b>ck\)-rule in the traditional donation game (see Ohtsuki et al. 2006).
Linear costs and benefits
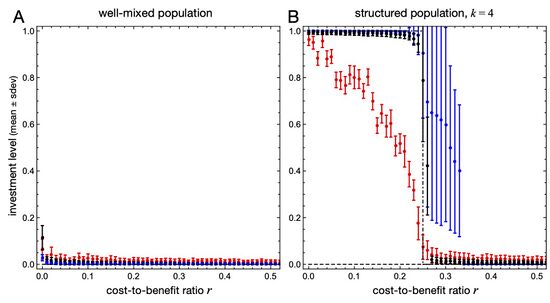
The evolutionary analysis becomes particularly simple for linear benefit and cost functions \(B(x)=x\) and \(C(x)=r x\), where \(r\) denotes the (marginal) cost-to-benefit ratio. Again, population structures are capable of supporting cooperation for sufficiently small \(r\). More precisely, the selection gradient \(D_\text{db}(x)=w\frac{k-2}{k(k-1)}(1-k r)\) is reduced to a constant (c.f. Eq. \eqref{eq:d:pd:dB}), and hence no singular strategy exists. However, the gradient changes sign for \(r^\ast=1/k\). Thus, for favourable cost-to-benefit ratios, \(r<r^\ast\), investments increase to their maximum, whereas for harsher conditions, \(r>r^\ast\) cooperative investments cannot be sustained, see Fig. 1.
Figure 1: Equilibrium investment levels (mean \(\pm\) standard deviation) in individual-based simulations of the linear continuous prisoner's dilemma (\(B(x)=x, C(x)=r x\)) as a function of the cost-to-benefit ratio, \(r\), for weak selection, \(w=1\) (red), moderate, \(w=10\) (black), and strong selection, \(w=100\) (blue). A in well-mixed populations with \(N=10^4\) individuals cooperative investments are close to zero regardless of \(r\) as predicted by adaptive dynamics (dashed line). The small variance further decreases for stronger selection emphasizing the disadvantage of mutants with higher investments. B for populations with \(k=4\) neighbours spatial adaptive dynamics predicts a threshold \(r^\ast=1/k\) (dash-dotted-line) below which investments reach the maximum but disappear above. Simulations on a \(100\times 100\) lattice confirm the trend but reveal an interesting susceptibility to noise: for weak selection (red) the maximum investment is not reached; intermediate selection (black) essentially follows pair approximation, while strong selection (blue) maintains non-zero investment levels beyond the predicted threshold. The large variation suggests co-existence of different traits and is confirmed through sample snapshots of the spatial configuration in Fig. 2i.
Interactive labs, Figure 1 A
|
Dynamics in well-mixed populations with size \(N=10^4\) for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as weak, moderate or strong selection, \(w=1, 10, 100\). The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| |||||
| well-mixed | \(w=1\) | \(w=10\) | \(w=100\) | ||
|---|---|---|---|---|---|
| \(r=0.1\) | |||||
| \(r=0.3\) | |||||
Interactive labs, Figure 1 B
|
Dynamics in on \(N=100\times100\) square lattices with \(k=4\) neighbours for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as weak, moderate or strong selection, \(w=1, 10, 100\). The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| |||||
| lattice, \(k=4\) | \(w=1\) | \(w=10\) | \(w=100\) | ||
|---|---|---|---|---|---|
| \(r=0.1\) | |||||
| \(r=0.3\) | |||||
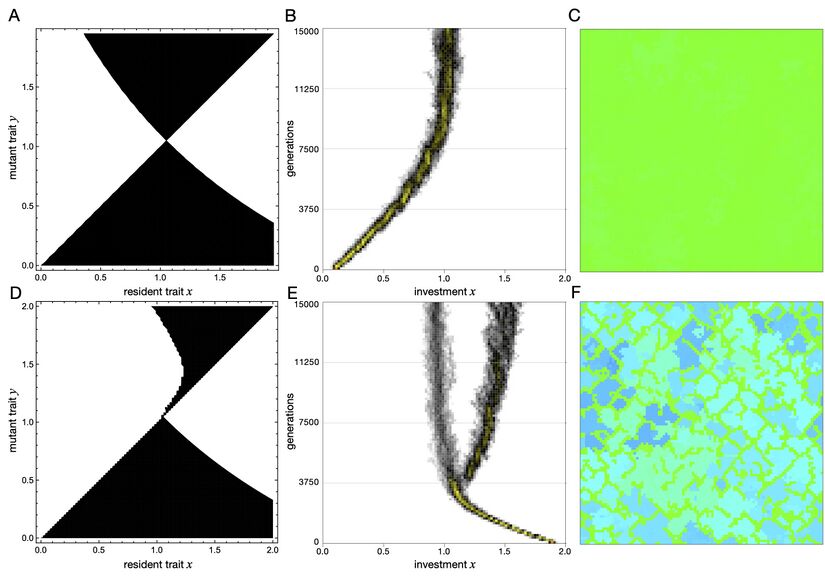
Interestingly, these analytical predictions are not always borne out in individual-based models when the selection strength, \(w\), is large. The reasons for the differences can be appreciated by looking at pairwise invasibility plots (\(PIP\)), which show the regions in \((x,y)\)-space in which a mutant \(y\) can invade a resident \(x\), i.e., regions for which the invasion fitness \(f(x,y)\) is positive. To construct these plots, we first solve the dynamical equation \(\dot q_{m|m}=0\) (see spatial adaptive dynamics) to find the equilibrium \(q^\ast_{m|m}\) for given resident and mutant trait values \(x, y\) and then determine the sign of the corresponding invasion fitness. An example is shown in Fig. 2g with \(r>1/k\) so that adaptive dynamics predicts evolution to pure defection.
Figure 2: Linear continuous prisoner's dilemma in \(100\times 100\) lattice populations with \(k=4\) neighbours. Evolutionary dynamics is illustrated for favourable cost-to-benefit ratios, \(r=0.1<1/k\) (A-C), and for harsher conditions, \(r=0.3>1/k\), with moderate selection, \(w=10\) (D-F) as well as strong selection, \(w=100\) (G–I). The left column shows the pairwise invasibility plots (\(PIP\)), which indicate whether mutant traits are capable of invading a particular resident population (white regions) or not (black regions). The middle column shows the evolutionary trajectory of the distribution of investments over time in individual-based simulations (darker shades indicate higher trait densities in the population with the highest densities in yellow). The right column depicts snapshots of the population configuration at the end of the simulation runs. The colour hue indicates the investment levels ranging from low (red) to intermediate (green) and high (blue). For \(r<1/k\) higher investors can always invade and eventually the maximum investment is reached (A–C), regardless of selection strength. The situation is reversed for \(r>1/k\) and weak to moderate selection where only lower investors can invade and investments dwindle to zero (D–F). Interestingly, for strong selection in lattice populations not only lower investors can invade for \(r>1/k\) but also those that invest significantly more than the resident (G–I). Note that the width of the region of unfavourable mutants decreases with increasing selection strength \(w\), i.e. the gap becomes easier to bridge (but does not depend on the resident trait \(x\); grey area for \(w=50\) and black area for \(w=100\)). Nevertheless adaptive dynamics predicts that investments evolve to zero because of the assumption that mutations are small, which restrict the dynamics to the diagonal of the \(PIP\). However, individual-based simulations show that rare larger mutations or a sequence of smaller ones can give rise to the co-existence of high and low investors. The outcome does not depend on the initial configuration of the population.
Interactive labs, Figure 2
|
Dynamics on a square \(100\times100\) lattice with \(k=4\) neighbours for favourable cost-to-benefit ratios, \(r=0.1<1/k\), and harsher conditions, \(r=0.3>1/k\), respectively, as well as moderate or strong selection, \(w=10, 100\). The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| ||||
| A-C: \(r=0.1\), \(w=10\) | D-F: \(r=0.3\), \(w=10\) | G-I: \(r=0.3\), \(w=100\) | ||
|---|---|---|---|---|
For mutants \(y\) sufficiently close to the resident \(x\), \(f(x,y)>0\) only holds for \(y<x\), so that evolution by (infinitesimally) small mutations, as envisaged in adaptive dynamics, indeed leads to ever smaller investment. However, the \(PIP\) also shows positive invasion fitness for mutants \(y>x\) if \(y\) is sufficiently larger than \(x\) (white area above the diagonal in Fig. 2g). In individual-based models, mutations are normally distributed around the parental trait and of finite size such that stochastically appearing larger mutations or sequences of smaller mutations in the right direction can give rise to the co-existence of high and low investors (see Fig. 2i). Thus, evolutionary diversification is possible in individual-based models despite the absence of evolutionary branching points in the adaptive dynamics, and even if the analytical prediction is evolution of pure defection. Note that this mode of evolutionary diversification is a feature of spatial structure that does not occur in the corresponding well-mixed models.
Saturating benefits
The continuous prisoner's dilemma was first introduced in Killingback et al. 1999 with saturating benefits \(B(x)=b_0\left( \exp{(-b_1 x)} \right)\) and linear costs \(C(x)=c_0 x\) (\(b_0, b_1, c_0>0\)). Using individual-based simulations these authors showed that structured populations are capable of supporting cooperation, whereas well-mixed populations are not. Spatial adaptive dynamics provides an analytical perspective on these results. For the given cost and benefit functions, we have: \begin{align} \label{eq:d:kdk:dB} D_\text{db}(x) &= w\frac{k-2}{k(k-1)}\left( b_0 b_1 e^{-b_1 x}-c_0 k\right)\\ \label{eq:cssess:kdk:dB} CS_\text{db}(x^\ast) &= ES_\text{db}(x^\ast) = -w\frac{k-2}{k-1}b_1 c_0<0. \end{align} There is a singular point at \begin{align} \label{eq:d:kdk:xast} x^\ast &= \frac1{b_1}\log\left(\frac{b_0 b_1}{c_0 k}\right). \end{align} The singular point is always convergence stable as well as evolutionarily stable (see Fig. 3b).
Figure 3: Continuous prisoner's dilemma with saturating benefits \(B(x)=b_0\left(1-\exp{(-b_1 x)}\right)\) and linear costs \(C(x)=c_0 x\) for \(b_0=8, b_1=1, c_0=0.7\) in \(100\times 100\) lattice populations for weak selection, \(w=1\) (top row) and strong selection, \(w=100\) (bottom row). The pairwise invasibility plots (\(PIP\), left column) show that higher investing mutants can invade for low resident investments and lower investing mutants can invade high investing residents. However, near the singular investment level, \(x^\ast=\log\left(\frac{b_0 b_1}{k c_0}\right)/b_1\approx1.050\), selection strength gives rise to interesting differences in the dynamics. A for weaker selection, \(w=1\), \(x^\ast\) is evolutionarily stable. This is confirmed through individual-based simulations. B depicts the investment distribution over time (darker shades indicate higher trait densities in the population with the highest densities in yellow). C shows a snapshot of the spatial configuration at the end of the simulation. The colour hue indicates the investment level ranging from low (red) to intermediate (green) to high (blue). In contrast, D for strong selection, \(w=100\), \(x^\ast\) can be invaded but only by higher investing mutants. As a consequence, a degenerate form of evolutionary branching may occur. Individual-based simulations confirm branching already for \(w=10\) (E, F).
Interactive labs, Figure 3
|
Dynamics on a square \(100\times100\) lattice with \(k=4\) neighbours for saturating benefits, \(B(x)=b_0\left(1-\exp{(-b_1 x)}\right)\) and linear costs \(C(x)=c_0 x\) for \(b_0=8, b_1=1, c_0=0.7\) with \(b_0=8, b_1=1, c_0=0.7\) with weak, \(w=1\) and stronger \(w=10\) selection. The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| |||
| A-C: weak selection \(w=1\) | D-F: stronger selection \(w=10\) | ||
|---|---|---|---|
Interestingly, the adaptive dynamics analysis again misses subtle but intriguing effects arising from strong selection. A pairwise invasibility plot for strong selection is shown in Fig. 3D) and reveals that \(x^\ast\) is susceptible to invasion by mutants with slightly higher investments. In individual-based models, this effectively turns \(x^\ast\) into a (degenerate) branching point, i.e., a starting point for evolutionary diversification. The diversification into coexisting high and low investors has already been observed in Killingback et al. 1999, but the underlying mechanism had not been addressed. The earlier results were based on a different, deterministic update rule, according to which a focal individual imitated the strategy of the best performing neighbour, including itself, but this update rule essentially corresponds to death-birth updating with very strong selection (the only difference being that the focal individual is removed). Hence the diversification reported in Killingback et al. 1999 is of the same type as the one seen here for strong selection.
Evolution in the continuous snowdrift game
In the continuous snowdrift game the payoff to an individual with strategy \(y\) interacting with an \(x\)-strategist is \(P(y,x)=B(x+y)-C(y)\). Note that this generalization to continuous strategies does not imply that every interaction between an individual with strategy \(x\) and another with strategy \(y\) invariably results in a snowdrift game. In fact, snowdrift games in this narrower sense appear only if the two traits \(x, y\) straddle the singular strategy \(x^\ast\). Depending on the cost and benefit functions, as well as on the strategies \(x\) and \(y\), any kind of \(2\times2\) game can arise, including a prisoner's dilemma, in which the lower investing strategy dominates (Doebeli et al. 2004, Doebeli et al. 2013). In this sense the framework of the continuous snowdrift game actually encompasses the gist of the continuous prisoner's dilemma for sufficiently high costs -- just as the classical snowdrift game turns into a prisoner's dilemma (see Hauert & Doebeli, 2004).
Following spatial adaptive dynamics, the selection gradient for the continuous snowdrift game in structured populations with death-birth updating is given by \begin{align} \label{eq:d:csd:dB} D_\text{db}(x) &= w\frac{k-2}{k(k-1)}\left((k+1)B^\prime(2x)-k C^\prime(x)\right). \end{align} Thus, singular strategies \(x^\ast\) may exist, and if \(x^\ast\) exists, it is convergence stable if \begin{align} \label{eq:css:csd:dB} CS_\text{db}(x^\ast) &= w\frac{k-2}{k(k-1)}\left(2(k+1)B^{\prime\prime}(2x^\ast)-k C^{\prime\prime}(x^\ast)\right)<0, \end{align} and evolutionarily stable if \begin{align} \label{eq:ess:csd:dB} ES_\text{db}(x^\ast) &= w\frac{k-2}{k^2(k-1)}\left((k+2)(k+1)B^{\prime\prime}(2x^\ast)-k^2 C^{\prime\prime}(x^\ast)\right)<0. \end{align} In particular, the conditions for convergence and evolutionary stability are different, which indicates the potential for evolutionary branching and hence the evolutionary emergence and co-existence of high investing cooperators and low investing defectors. The above conditions are the spatial analogs of the analysis for well-mixed continuous snowdrift games reported in Doebeli et al. 2004. Also note that for linear cost and benefit functions it is not possible to satisfy all constraints for the continuous snowdrift game and hence the simplest case is given by quadratic costs and benefits.
Quadratic costs and benefits
For suitable cost and benefit functions the (spatial) adaptive dynamics is analytically accessible. Here we focus on the quadratic cost and benefit functions used in Doebeli et al. 2004 for the well-mixed case: \(B(x)=b_1 x+b_2 x^2\) and \(C(x)=c_1 x+c_2 x^2\). We assume that the evolving trait is confined to the interval \([0,1]\). The benefit and cost functions satisfy the criteria \(B(0)=C(0)=0\), \(B(x),C(x)\geq0\) and \(B^{\prime\prime}(x)<0\) for \(x\in[0,1]\) provided that \(b_1,c_1>0\), \(b_2,c_2<0\) as well as \(b_1<-4b_2\) and \(c_1<-2c_2\). The first two conditions ensure that costs and benefits are increasing yet saturating, while the latter two ensure that \(B(2x)\) and \(C(x)\) are increasing over the entire trait interval, i.e. their respective maximum occurs for \(x\geq1\).
For small resident values \(x\), the selection gradient \eq{d:csd:dB} becomes \(D_\text{db}(x)\approx w\frac{k-2}{k(k-1)}\left((k+1)b_1-k c_1\right)\), and hence cooperative investments evolve away from zero provided that \(b_1>\frac{k}{k+1}c_1\), which is slightly less restrictive than the corresponding condition \(b_1>c_1\) in the well-mixed case.
For the above quadratic costs and benefits the singular strategy is given by \begin{align} \label{eq:xs:csd:dB} x^\ast_\text{db} &= \frac{b_1(k+1)-c_1 k}{2c_2k-4b_2(k+1)}. \end{align} The numerator of Eq. \eqref{eq:xs:csd:dB} is positive if and only if the condition for evolution away from zero, \(b_1>\frac{k}{k+1}c_1\), is satisfied. Similarly, the denominator of Eq. \eqref{eq:xs:csd:dB} is positive if and only if \(2b_2(k+1)<c_2k\) (recall \(b_2, c_2<0\)). It is clear from Eq. \eqref{eq:css:csd:dB} that this is also the condition for convergence stability. Thus, if a singular point, \(x^\ast\), exists, cooperative traits either evolve away from zero and \(x^\ast\) is convergence stable, or the trait cannot evolve away from zero and \(x^\ast\) is a repellor.
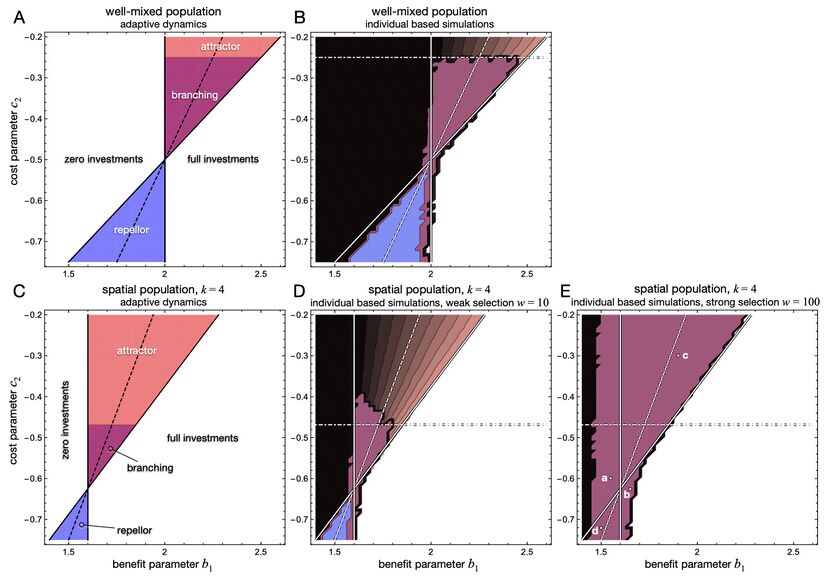
We note that if the singular point exists, \(x^\ast\), it is shifted towards smaller investments for a given set of parameters, as compared to well-mixed populations with the same parameters: \(x^\ast = \frac{b_1-c_1}{2c_2-4b_2}\). Furthermore, the condition for convergence stability, \(2b_2(k+1)<c_2k\), is less restrictive than the corresponding condition \(2b_2<c_2\) in the well-mixed case. Finally, from \eq{ess:csd:dB} we see that the condition for evolutionary stability is \(b_2(k+2)(k+1)<c_2 k^2\), which is again less restrictive than the corresponding condition \(b_2<c_2\) in the well-mixed case. Combining the two stability conditions shows that evolutionary branching occurs for \(2b_2(k+1)/k<c_2<b_2(k+1)(k+2)/k^2\). Thus, the analytical approach based on pair approximation suggests that population structures tend to inhibit evolutionary diversification by decreasing the range of parameters for which the singular point is an evolutionary branching point (c.f. Fig. 4A & C).
Figure 4: Continuous snowdrift game with quadratic benefit and cost functions, \(B(x)=b_1 x+b_2 x^2\) and \(C(x)=c_1 x+c_2 x^2\). Evolutionary outcomes are shown as a function of the benefit parameter \(b_1\) and cost parameter \(c_2\) with \(b_2=-1/4\) and \(c_1 = 2\). Note that \(b_1<2\) violates the assumption \(B(x)>C(x)\) at least for small \(x\) and hence effectively mimics the characteristics of the prisoner's dilemma. A analytical predictions based on adaptive dynamics in well-mixed populations and B results from individual-based simulations for populations with \(N=10^4\) individuals. C analytical predictions based on spatial adaptive dynamics and complementing individual-based simulations on \(100\times 100\) lattices for D moderate selection, \(w=10\), and E strong selection, \(w=100\). In lattice populations the parameter region admitting singular strategies is shifted to both smaller values of \(b_1\) and of \(c_2\) and the size of the region admitting evolutionary branching is markedly smaller than in well-mixed populations (< strong>A, C). Interestingly, spatial adaptive dynamics predicts branching only for parameters where defection dominates in well-mixed populations, \(b_1<c_1\), mimicking the continuous prisoner's dilemma. For weak to moderate selection predictions by adaptive dynamics (A, C) are in good agreement with results from individual-based simulations (B, D), where equilibrium investment levels range from the minimum (black) to intermediate (grey) and the maximum (white) augmented by convergence stability (red) and evolutionary instability (blue) with the overlapping region indicating evolutionary branching (maroon) in adaptive dynamics and diversification in simulations. For strong selection (E) striking differences arise with a much increased region of diversification. The points labelled a-d indicate the parameter settings for the invasion analysis in Fig. 5. Note that the automated classification of investment distributions becomes more difficult whenever the singular investment \(x^\ast\) is close to zero or one.
The results for well-mixed populations summarized in Fig. 4A & B can be replicated and verified in the tutorial Origin of Cooperators and Defectors. The following labs illustrate the dynamical regimes in spatially structured populations.
Interactive labs, Figure 4
|
Dynamical regimes in the spatial continuous snowdrift game for moderate selection, \(w=10\), on \(N=100\times100\) square lattices with \(k=4\) neighbours. The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| |||
| branching, \(c_2=-0.5,b_1=1.65\) | |||
|---|---|---|---|
| attractor, \(c_2=-0.3,b_1=1.9\) | |||
| repellor, \(c_2=-0.75,b_1=1.5\) | |||
| zero investments, \(c_2=-0.5,b_1=1.5\) | |||
| full investments, \(c_2=-0.5,b_1=2\) | |||
Strong selection greatly enhance the parameter region resulting in a diversity of traits, see Fig. 4E. The parameter combinations marked with points a,b,c,d refer to modes of diversification that do not rely on evolutionary branching and only occur in spatially structured populations.
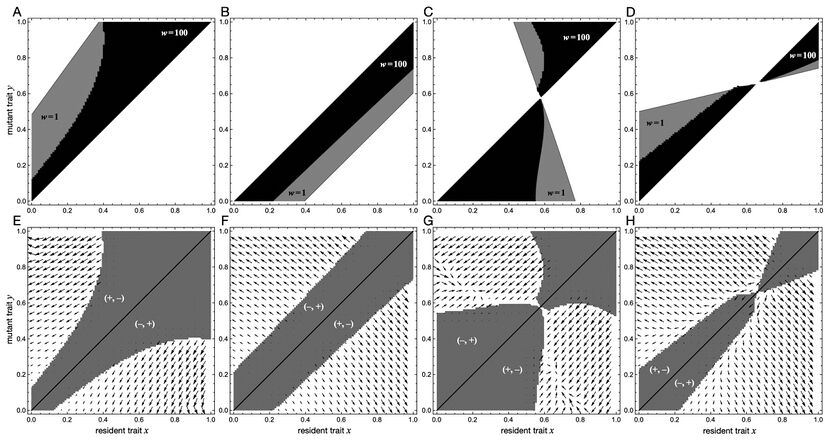
Figure 5: Spatial modes of diversification in the continuous snowdrift game with quadratic benefit and cost functions.
A-D depict pairwise invasibility plots (PIP, top row) for the four scenarios illustrating increased spatial diversification due to strong selection (c.f. parameter combinations a-d marked in Fig. 4). In all cases the width of the region of disadvantageous mutants decreases with selection strength (grey for \(w=1\); black for \(w=100\)).
A the PIP suggests gradual evolution towards minimal investments, except for smaller resident traits, where not only lower investing mutants can invade but also those making markedly higher investing.
B higher investing mutants can always invade, but so can traits investing markedly less.
C selection strength distorts the PIP in the vicinity of the convergence and evolutionarily stable \(x^\ast\) resulting in a degenerate form of branching (c.f. Fig. 3).
D the PIP indicates that \(x^\ast\) is a repellor such that residents with \(x<x^\ast\) are invaded by lower investors while those with \(x>x^\ast\) by higher investors. However, as a consequence of strong selection, mutants with markedly higher (lower) investments can also invade.
E-H depict corresponding plots of regions of mutual invasibility (PIP\(^\text{2}\), white regions). Regions where mutants or residents are unable to invade (grey) are marked with \((+,-)\) and \((-,+)\), respectively. The vector field shows the evolutionary divergence and indicates the direction of selection for two co-existing residents based on analytical approximations of the spatial invasion dynamics. In all cases divergence drives the traits away from the diagonal and hence preserves diversity.
Parameters: \(b_2=-1/4, c_1=2\), A \(b_1=1.55\), \(c_2=-0.6\); B \(b_1=1.65\), \(c_2=-0.625\); C \(b_1=1.9\), \(c_2=-0.3\); D \(b_1=1.5\), \(c_2=-0.72\).
Interactive labs, Figure 5
|
Modes of diversification in the spatial continuous snowdrift game. The parameter settings refer to points a,b,c,d in Fig. 4E. The interactive labs below illustrate the trait distribution over time where the colours indicate the trait density according to:
| |||
| Figure 5A & E, Figure 4E a, \(c_2=-0.6,b_1=1.55\) | |||
|---|---|---|---|
| Figure 5B & F, Figure 4E b, \(c_2=-0.625,b_1=1.65\) | |||
| Figure 5C & G, Figure 4E c, \(c_2=-0.3,b_1=1.9\) | |||
| Figure 5D & H, Figure 4E d, \(c_2=-0.72,b_1=1.5\) | |||
Conclusions & Discussion
In all scenarios considered here we find that population structures can promote and facilitate spontaneous diversification in social dilemmas into high and low investors, especially when selection is strong. However, at the same time, classical evolutionary branching tends to be inhibited, but compensated for by other modes of diversification. We derive an extension of adaptive dynamics for continuous games in (spatially) structured populations based on pair approximation, which tracks the frequencies of mutant-resident pairs during invasion. It turns out that predictions derived from this spatial adaptive dynamics framework are independent of selection strength. More precisely, selection strength only scales the magnitude of the selection gradient as well as that of convergence and evolutionary stability but neither affects the location of singular strategies nor their stability. Nevertheless, from the invasion analysis of mutant traits \(y\) into resident populations \(x\), as well as from individual-based simulations, it is clear that selection strength has a significant impact on the dynamics in general, and on diversification in particular. During the invasion process the local configuration probability of mutant pairs \(q_{m|m}\) is of crucial importance and changes with selection strength, see \eq{qmm:dB:sol}. However, in the adaptive dynamics limit \(y\to x\) the pair configuration probability reduces to a constant \(q_{m|m}\to1/(k-1)\). Even though this is the same value as obtained in the limit of weak selection, \(w\to0\), it is important to note that the limit \(y\to x\) does not necessarily imply weak selection. Thus, the different modes of diversification cannot be understood based on spatial adaptive dynamics alone but require a more comprehensive analysis of invasion dynamics.
Structured populations offer new modes of diversification that are driven by an interplay of finite-size mutations and population structures. Trait variation is more easily maintained in structured populations due to the slower spreading of advantageous traits as compared to well-mixed populations. Spatial adaptive dynamics is unable to capture these new modes of diversification because of the underlying assumption that the resident population is composed of discrete traits (monomorphic before branching and dimorphic or polymorphic after branching). Nevertheless, invasion analysis and pairwise invasibility plots, \(PIP\), in particular, provide an intuitive interpretation for additional pathways to diversification that are introduced by spatial structures and further promoted for increasing selection strength. Even in the vicinity of evolutionarily stable investments, trait combinations exist that admit mutual invasion and hence can coexist. However, such states cannot evolve through adaptive dynamics but are nevertheless accessible to trait distributions around the evolutionarily stable trait and can drive a degenerate form of branching. Moreover, spatial invasion fitness can open up new regions in trait space for mutant invasion. However, those regions need not be accessible by small mutational steps, and instead require stochastically appearing larger mutations or sequences of smaller mutations that allow to bridge regions of unfavourable traits.
Previous attempts at amalgamating adaptive dynamics and spatial structure have not observed spontaneous diversification or evolutionary branching. In particular, Allen et al. (2013) augment adaptive dynamics by structure coefficients (Tarnita et al. 2011), which restrict the analysis to weak selection. Moreover, their framework is fundamentally different from ours because it is based on fixation probabilities rather than invasion fitness. More specifically, their analysis is based on the fixation probabilities \(p_x\) and \(p_y\) of two types \(x\) and \(y\) in a population consisting of \(x\) and \(y\): \(x\) is favoured over \(y\) if \(p_x>p_y\) (see Eq. 4 and formulas following Eq. 7 in Allen et al. 2013). Clearly, it is then impossible to have both types be favoured in an \((x,y)\)-population, but this is exactly the requirement for mutual coexistence. In fact, Allen et al. acknowledge that fixation probabilities are "less appropriate" for studying evolutionary branching and that instead "establishment probabilities" should be considered for studying diversification. As a consequence their adaptive dynamics derivation precludes its most intriguing feature, that of evolutionary branching. However, in the limit of weak selection the two approaches are compatible in some aspects. For example, the selection gradient and the condition for convergence stability reported for the continuous prisoner's dilemma are identical (c.f. Eqs. \eqref{eq:d:csd:dB}, \eqref{eq:css:csd:dB} and their Eqs. (11), (13)). In our framework, the use of invasion fitness allows to determine evolutionary stability, and the corresponding \(PIP\)'s reveal the potential for degenerate forms of branching – but only for stronger selection (see Fig. 3). Another attempt at spatial adaptive dynamics considers spatial structure in the form of demes (Parvinen et al. 2017). However, quite naturally such deme structures suppress branching because in the long run it is impossible to maintain multiple co-existing traits in small demes, which quickly become homogeneous. Instead, branching is only possible if demes are large enough to support branching in every single one.
Interestingly, in well-mixed populations evolutionary branching is only observed for the continuous snowdrift game, where two distinct traits of high and low investors can co-exist and essentially engage in a classical (discrete) snowdrift game. In contrast, in structured populations with death-birth updating, evolutionary branching is only observed for prisoner's dilemma type interactions where lower investments invariably dominate higher ones, which applies both in the continuous prisoner's dilemma as well as the continuous snowdrift game with sufficiently high costs. The reason for this surprising difference can be understood intuitively by considering the preferred spatial configurations in the two classical (discrete) games: in the prisoner's dilemma cooperators form compact clusters to reduce exploitation by defectors (minimize surface), while in the snowdrift game filament like clusters form because it is advantageous to adopt a strategy that is different from that of the interaction partners (maximize surface). In the continuous variants of those games it is naturally much harder to maintain and spread distinct traits in fragmented filament-like structures because they are more prone to effects of noise than compact clusters. Effectively this fragmentation inhibits evolutionary branching because diverging traits tend to trigger further fragmentation and as a consequence do not survive long enough to get established and form their own branch. In contrast, the compact clusters promoted by the prisoner's dilemma provide structural protection for higher investors and thus help drive diversification.
Because of global competition the spatial dynamics for birth-death updating is (unsurprisingly) much closer to results for well-mixed populations. For example, evolutionary branching was again only observed for continuous snowdrift game. Also because of global competition, structured populations are updated in a non-uniform manner. In particular, regions of high payoffs experience a much higher turnover than regions of low payoffs. For strong selection this can result in almost frozen parts of the population. As a consequence unsuccessful traits are able to stay around for long times and, in some cases, those traits turn out to be advantageous again at later times when the surroundings have sufficiently changed, so that the stragglers then contribute to diversification. This mode of diversification, however, introduces historical contingencies where the evolutionary end state can sensitively depend on the initial configuration.
Overall, we find that evolutionary diversification is a robust feature of continuous spatial games, and that spatial structure can sometimes hinder, but generally promotes diversification through modes of diversification that complement traditional evolutionary branching.
Publications
- Hauert, C. & Doebeli, M. (2021) Spatial social dilemmas promote diversity, Proc. Natl. Acad. Sci. USA 118 42 e2105252118 doi: 10.1073/pnas.2105252118
References
- Allen, B., Nowak, M.A., & Dieckmann, U. (2013) Adaptive dynamics with interaction structure. Am. Nat. 181 (6) E139–E163.
- Doebeli M, Hauert C, Killingback T (2004) The evolutionary origin of cooperators and defectors. Science 306 (5697) 859–62.
- Doebeli M, Hauert C, Killingback T (2013) A comment on "Towards a rigorous framework for studying 2-player continuous games" by Shade T. Shutters, Journal of Theoretical Biology 321, 40--43, 2013. J. Theor. Biol. 336 240–241.
- Hauert C, Doebeli M (2004) Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428 643–646.
- Killingback, T., Doebeli, M., & Knowlton, N. (1999) Variable investment, the continuous prisoner's dilemma, and the origin of cooperation. Proc. R. Soc. B 266 1723–1728.
- Ohtsuki, H., Hauert, C., Lieberman, E., & Nowak, M.A. (2006) A simple rule for the evolution of cooperation on graphs. Nature 441 502–505.
- Parvinen, K., Ohtsuki, H., & Wakano, J.Y. (2017) The effect of fecundity derivatives on the condition of evolutionary branching in spatial models. J. Theor. Biol. 416 129–143.
- Tarnita, C.E., Wage, N., & Nowak, M.A. (2011) Multiple strategies in structured populations. Proc. Natl. Acad. Sci. USA 108 2334–2337.