EvoLudo: Difference between revisions
No edit summary |
No edit summary |
||
| Line 23: | Line 23: | ||
<div class="footnote" style="font-size:smaller"> | <div class="footnote" style="font-size:smaller"> | ||
Hauert, C., & Szabó, G. (2024) ''PNAS Nexus'' (in print). <!--'''462''' 347-360 [https://doi.org/10.1016/j.jtbi.2018.11.019 doi: 10.1016/j.jtbi.2018.11.019]--> | Hauert, C., & Szabó, G. (2024) ''PNAS Nexus'' (in print). <!--'''462''' 347-360 [https://doi.org/10.1016/j.jtbi.2018.11.019 doi: 10.1016/j.jtbi.2018.11.019]--> | ||
</div> | |||
|} | |||
{{-}} | |||
=== <!--[[-->Spatial social dilemmas promote diversity<!--]]--> === | |||
{| | |||
| style="vertical-align:top" |[[Image:Spatial social dilemmas promote diversity.jpg|160px|left<!--|link=Spatial social dilemmas promote diversity-->]] | |||
| style="vertical-align:top" | | |||
''Upcoming:'' new tutorial on <!--[[Spatial social dilemmas promote diversity|-->modes of spontaneous diversification in spatial settings<!--]]--> in preparation. | |||
Evolutionary branching and diversification in interactions with continuous behavioral traits is important for under- standing the emergence of distinct, discrete, and coexisting strategies. In social dilemmas, this suggests an evolutionary pathway for the origin of cooperators and defectors. Here we study evolutionary diversification in structured populations and identify mechanisms driving spontaneous and persistent diversification. Through analytical and numerical techniques, we demonstrate that spatial structure admits new modes of diversification that complement classical evolution- ary branching. In particular, when selection is strong, diversification tends to occur more readily than in unstructured populations. | |||
<div class="footnote" style="font-size:smaller"> | |||
Hauert, C., & Doebeli, M. (2021) ''PNAS'' '''118''' 42 e2105252118 [https://doi.org/10.1073/pnas.2105252118 doi: 10.1073/pnas.2105252118]. | |||
</div> | </div> | ||
|} | |} | ||
Revision as of 08:56, 21 August 2024
EvoLudo is a growing collection of interactive tutorials that complement numerous research articles on evolutionary games (ludo Latin for "I play" or Italian for "game"). These tutorials allow the reproduction and verification of results reported in scientific articles. In addition, they are intended to encourage the interested reader, students and researchers to explore the fascinating world of game theory and evolutionary dynamics in a playful manner. This helps to develop a better intuitive understanding of the often complex evolutionary dynamics and encourage further explorations in the fascinating and often mesmerizing world of spatio-temporal patterns.
In 2012 the EvoLudo wiki was introduced as the successor of the VirtualLabs, which were originally hosted by the University of Vienna. The VirtualLabs pages have been retired partly because the interactive tutorials were based on the long obsolete technology of java applets. The adventurous and fearless are welcome to visit the archived pages. Over the 10 years since their initial instalment in 2002 the VirtualLabs have attracted over 250k visitors (which was significant back in the day).
The VirtualLabs, and EvoLudo by extension, have been encouraged and inspired by Karl Sigmund during my post-doc under his mentorship.
The EvoLudo wiki is created and maintained by Christoph Hauert. Feedback, suggestions and contributions are most welcome.
Tutorials
Mutualisms: cooperation between species
Spatial social dilemmas promote diversity
 |
Upcoming: new tutorial on modes of spontaneous diversification in spatial settings in preparation. Evolutionary branching and diversification in interactions with continuous behavioral traits is important for under- standing the emergence of distinct, discrete, and coexisting strategies. In social dilemmas, this suggests an evolutionary pathway for the origin of cooperators and defectors. Here we study evolutionary diversification in structured populations and identify mechanisms driving spontaneous and persistent diversification. Through analytical and numerical techniques, we demonstrate that spatial structure admits new modes of diversification that complement classical evolution- ary branching. In particular, when selection is strong, diversification tends to occur more readily than in unstructured populations. Hauert, C., & Doebeli, M. (2021) PNAS 118 42 e2105252118 doi: 10.1073/pnas.2105252118. |
Evolutionary graph theory
 |
Tutorial on evolutionary graph theory, which provides a formal approach to describe the spreading and fixation (or extinction) of a mutant type in structured populations. Interestingly, the fixation probabilities remain unaffected by the underlying structure for a large class of graphs. However, some graphs may act either as amplifiers or suppressors of selection by increasing or decreasing the fixation probabilities as compared to unstructured populations. In contrast, fixation and absorption times are very sensitive to changes in the graph structure and hence vary greatly even for graphs that leave fixation probabilities unchanged. Even though fixation times are, in general, not preserved between graphs, symmetries of a graph can at least ensure that fixation times do not depend on the initial location of the mutant. This summarizes research efforts that span over a decade, including:
|
Stochastic dynamics in finite populations
 |
Tutorial on the stochastic dynamics arising through demographic noise and mutations in finite populations of size \(N\). Comparisons of the deterministic replicator dynamics in the limit of infinite population sizes \(N\to\infty\) to the stochastic dynamics generated by stochastic differential equations, which are derived from a microscopic description of elementary changes in the population, as well as to results from individual based simulations.
|
Evolutionary Games and Population Dynamics
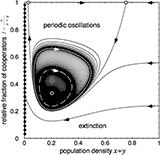 |
Tutorial on frequency dependent selection in populations of varying size. The classic replicator dynamics assumes constant (infinite) population sizes and thus neglects the ecology of the population. Linking ecological dynamics and evolutionary games generates fascinating and rich dynamical behavior. Most importantly, however, this reveals a new mechanism for maintaining cooperation through negative feedback between population densities and the size of interaction groups.
|
Origin of Cooperators and Defectors
 |
Tutorial on the gradual evolution of distinct cooperative and defective behavioral patterns through evolutionary branching into separate trait groups characterized by high and low cooperative investments. This is based on a model that extends the classical Snowdrift game to continuously varying degrees of cooperation. Apart from evolutionary branching, this model exhibits rich dynamics that can be easily explored using this interactive tutorial.
|
2×2 Games
 |
Tutorial on 2×2 games in populations with different structures. 2×2 games describe a rich set of pairwise interactions among individuals. The most prominent game is certainly the Prisoner's Dilemma which has become the paradigm to discuss the emergence of cooperative behavior. If players are arranged on regular lattices, many of these games produce fascinating spatio-temporal patterns. This tutorial provides a hands-on experience of this dynamical world.
|
News
August 2024 MediaWiki software updated and looks modernized. EvoLudo simulations updated.
October 2023 EvoLudo simulation toolkit extended and MediaWiki software updated and general maintenance. The API documentation of the EvoLudo simulation toolkit is now available. Plans to release the source code into the public domain are in progress - stay tuned.
October 2016 EvoLudo simulation toolkit updated. The simulations are now resizable, fullscreen is improved (still beta, though) and context menu offers snapshots and the statistical data can be exported.
August 2016: New tutorial on evolutionary graph theory added. This includes significant extensions and improvements of the EvoLudo labs to do statistical analysis over several simulation runs to determine fixation probabilities and fixation times.
June 2016: 3D capabilities added to the interactive EvoLudo labs using WebGL! Check out the 3D representations of population structures. If you have your red-cyan glasses ready, the structures can be viewed even in real 3D (use context menu). In addition some fullscreen capabilities have been added but this feature is still under construction - stay tuned.
March 2016: EvoLudo revamped! Java applets have been retired and, as a welcome side-effect, the interactive tutorials are now finally also accessible from tablets and other mobile devices. This major update of the EvoLudo simulation and visualization framework has been made possible through my sabbatical leave from UBC and facilitated by an extended research visit of Arne Traulsen's group at the Max-Planck Institute for Evolutionary Biology in Plön, Germany.
Highlights

|
ClassicsClassic patterns generated by the spatial prisoner's dilemma and first published by Nowak, M. A. & May, R. M. Nature 359 826-829 (1992). Spatial structure enables cooperators (blue, green) survive under conditions where otherwise defectors (red, yellow) would take over. Through spatial clustering cooperators interact more frequently with other cooperators and reduce exploitation by defectors. |

|
ModernSpatial heterogeneity promotes cooperation based on different types of pattern formation processes driving the density distribution of cooperators (green) and defectors (red). Individuals can migrate (diffuse) in order to populate empty territories (black). Slow diffusion of cooperators fosters aggregation in highly productive patches (activation), whereas fast diffusion enables defectors to readily locate and exploit these patches (inhibition). These antagonistic forces promote co-existence of cooperators and defectors in static or dynamic patterns, including spatial chaos of ever changing configurations |

|
ArtsInstallation "Evolution" on the NOVA, the world's largest true 3D display in the main train station in Zürich, Switzerland. The installation was created in collaboration with media artist Chandrasekhar Ramakrishnan and is based on the EvoLudo simulation toolkit. “Evolution” was presented in September 2009 in honour of Darwin's bicentenary and became part of the permanent collection until NOVA was retired in 2012. The NOVA display is a 5×5×1m cube of 25,000 LED lights and displays the competition of cooperators (blue, green) and defectors (red, yellow) in the prisoner’s dilemma in 3D unfolding as an evolutionary kaleidoscope. |

