Stochastic dynamics in finite populations: Difference between revisions
No edit summary |
No edit summary |
||
| Line 23: | Line 23: | ||
===Deterministic Dynamics=== | ===Deterministic Dynamics=== | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - ODE.svg|left|200px]] | [[Image:RSP - ODE.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - ODE]] | ||
====[[EvoLudoLab: Rock-Paper-Scissors - ODE|Replicator dynamics]]==== | ====[[EvoLudoLab: Rock-Paper-Scissors - ODE|Replicator dynamics]]==== | ||
In the limit <math>N\to\infty</math> with <math>s=1.4</math> and without mutations, <math>\mu=0</math>, <math>\hat x</math> is an attractor of the replicator dynamics. The figure shows a sample trajectory that spirals towards the interior fixed point <math>\hat x</math>. | In the limit <math>N\to\infty</math> with <math>s=1.4</math> and without mutations, <math>\mu=0</math>, <math>\hat x</math> is an attractor of the replicator dynamics. The figure shows a sample trajectory that spirals towards the interior fixed point <math>\hat x</math>. | ||
| Line 30: | Line 30: | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - ODE Mutations.svg|left|200px]] | [[Image:RSP - ODE Mutations.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - ODE with Mutations]] | ||
==== [[EvoLudoLab: Rock-Paper-Scissors - ODE with Mutations|Replicator-Mutator dynamics]]==== | ==== [[EvoLudoLab: Rock-Paper-Scissors - ODE with Mutations|Replicator-Mutator dynamics]]==== | ||
Including mutations in the replicator dynamics gives rise to the replicator-mutator dynamics. Mutations destabilizes the interior fixed point <math>\hat x</math> an can give rise to stable limit cycles. The image shows a sample trajectory for <math>\mu=0.002</math>. | Including mutations in the replicator dynamics gives rise to the replicator-mutator dynamics. Mutations destabilizes the interior fixed point <math>\hat x</math> an can give rise to stable limit cycles. The image shows a sample trajectory for <math>\mu=0.002</math>. | ||
| Line 38: | Line 38: | ||
===Stochastic Dynamics=== | ===Stochastic Dynamics=== | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - SDE.svg|left|200px]] | [[Image:RSP - SDE.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - SDE]] | ||
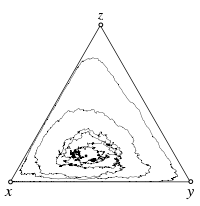
==== [[EvoLudoLab: Rock-Paper-Scissors - SDE|Stochastic differential equations]]==== | ==== [[EvoLudoLab: Rock-Paper-Scissors - SDE|Stochastic differential equations]]==== | ||
{{-}} | {{-}} | ||
| Line 44: | Line 44: | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - SDE Mutations.svg|left|200px]] | [[Image:RSP - SDE Mutations.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - SDE with Mutations]] | ||
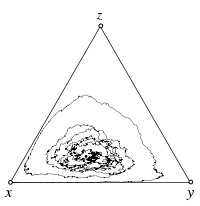
==== [[EvoLudoLab: Rock-Paper-Scissors - SDE with Mutations|Stochastic differential equations, with mutations]]==== | ==== [[EvoLudoLab: Rock-Paper-Scissors - SDE with Mutations|Stochastic differential equations, with mutations]]==== | ||
{{-}} | {{-}} | ||
| Line 51: | Line 51: | ||
===Individual Based Simulations=== | ===Individual Based Simulations=== | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - IBS.svg|left|200px]] | [[Image:RSP - IBS.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - IBS]] | ||
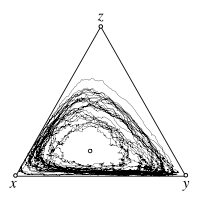
==== [[EvoLudoLab: Rock-Paper-Scissors - IBS|Individual based simulations]]==== | ==== [[EvoLudoLab: Rock-Paper-Scissors - IBS|Individual based simulations]]==== | ||
{{-}} | {{-}} | ||
| Line 57: | Line 57: | ||
<div class="lab_description SDE"> | <div class="lab_description SDE"> | ||
[[Image:RSP - IBS Mutations.svg|left|200px]] | [[Image:RSP - IBS Mutations.svg|left|200px|link=EvoLudoLab: Rock-Paper-Scissors - IBS with Mutations]] | ||
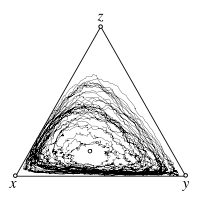
==== [[EvoLudoLab: Rock-Paper-Scissors - IBS with Mutations|Individual based simulations, with mutations]]==== | ==== [[EvoLudoLab: Rock-Paper-Scissors - IBS with Mutations|Individual based simulations, with mutations]]==== | ||
{{-}} | {{-}} | ||
Revision as of 23:11, 10 March 2012
Stochastic differential equations (SDE) provide a general framework to describe the evolutionary dynamics of an arbitrary number of types in finite populations, which results in demographic noise, and to incorporate mutations. For large, but finite populations this allows to include demographic noise without requiring explicit simulations. Instead, the population size only rescales the amplitude of the noise. Moreover, this framework admits the inclusion of mutations between different types, provided that mutation rates, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , are not too small compared to the inverse population size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/N} . This ensures that all types are almost always represented in the population and that the occasional extinction of one type does not result in an extended absence of that type. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu N\ll1} this limits the use of SDE’s, but in this case well established alternative approximations are available based on time scale separation. We illustrate our approach by a Rock-Scissors-Paper game with mutations, where we demonstrate excellent agreement with simulation based results for sufficiently large populations. In the absence of mutations the excellent agreement extends to small population sizes.
This tutorial complements a series of research articles by Arne Traulsen, Jens Christian Claussen & Christoph Hauert
Rock-Paper-Scissors game
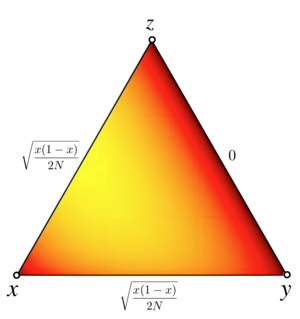
Comparisons between the deterministic dynamics in infinite populations, the stochastic dynamics in finite populations and individual based simulations focus on the Rock-Paper-Scissors game with a generic payoff
According to the replicator equation the game exhibits saddle node fixed points at , and as well as an interior fixed point at independent of the parameter . For , is a stable focus and an unstable focus for . In the non-generic case the dynamics exhibits closed orbits.
Deterministic Dynamics
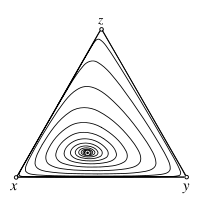
Replicator dynamics
In the limit with and without mutations, , is an attractor of the replicator dynamics. The figure shows a sample trajectory that spirals towards the interior fixed point .
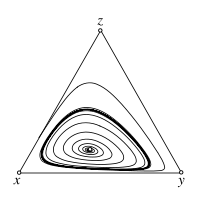
Replicator-Mutator dynamics
Including mutations in the replicator dynamics gives rise to the replicator-mutator dynamics. Mutations destabilizes the interior fixed point an can give rise to stable limit cycles. The image shows a sample trajectory for .
Stochastic Dynamics
Individual Based Simulations
From finite to infinite populations
In unstructured, finite populations of constant size, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} , consisting of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} distinct strategic types and with a mutation rate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , evolutionary changes can be described by the following class of birth-death processes: In each time step, one individual of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} produces a single offspring and displaces another randomly selected individual of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} . With probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-\mu} , no mutation occurs and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} produces an offspring of the same type. But with probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , the offspring of an individual of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\neq j} ) mutates into a type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} individual. This results in two distinct ways to increase the number of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} types by one at the expense of decreasing the number of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} types by one, hence keeping the population size constant. Biologically, keeping Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} constant implies that the population has reached a stable ecological equilibrium and assumes that this equilibrium remains unaffected by trait frequencies. The probability for the event of replacing a type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} individual with a type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} individual is denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{kj}} and is a function of the state of the population Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf X=(X_1, X_2, \ldots X_d)} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_n} indicating the number of individuals of type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textstyle\sum_{n=1}^d X_n = N} .
For such processes we can easily derive a Master equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^{\tau+1}({\mathbf X}) = P^{\tau}({\mathbf X})+\!\sum_{j,k=1}^d\! P^{\tau}({\mathbf X}_j^k) T_{kj}({\mathbf X}_j^k)-P^{\tau}({\mathbf X})\ T_{jk}({\mathbf X}))}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^\tau({\mathbf X})} denotes the probability of being in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf X} at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbf X}_j^k=(X_1, \ldots X_j-1, \ldots X_k+1, \ldots X_d)} represents a state adjacent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf X} . For large but finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} the Kramers-Moyal expansion yields a convenient approximation in the form of a Fokker-Planck equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot \rho({\mathbf x}) = -\sum_{k=1}^{d-1}\frac{\partial}{\partial x_k}\rho({\mathbf x}){\mathcal A}_{k}({\mathbf x})+\frac12\sum_{j,k=1}^{d-1}\frac{\partial^2}{\partial x_k\partial x_j}\rho({\mathbf x}){\mathcal B}_{jk}({\mathbf x})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbf x} = {\mathbf X}/N} represents the state of the population in terms of frequencies of the different strategic types and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho({\mathbf x})} is the probability density in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf x} . The drift vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_{k}({\mathbf x})} is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_{k}({\mathbf x}) = \sum_{j=1}^{d} \Big(T_{j k}({\mathbf x}) - T_{k j}({\mathbf x}) \Big) = -1+\sum_{j=1}^{d} T_{j k}({\mathbf x})}
For the second equality we have used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textstyle\sum_{j=1}^d T_{kj}({\boldsymbol x})=1} , which simply states that a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -type individual transitions to some other type (including staying type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} ) with probability one. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal A}_{k}({\mathbf x})} is bounded in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [-1, d-1]} because the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{jk}} are probabilities.
The diffusion matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal B}_{jk}({\mathbf x})} is defined as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}{\mathcal B}_{jk}({\mathbf x}) &= - \frac{1}{N} \left[ T_{j k}({\mathbf x}) + T_{k j}({\mathbf x}) \right] \quad {\rm for} \quad j \neq k \\ {\mathcal B}_{jj}({\mathbf x}) &= \frac{1}{N} \sum_{l=1,l\neq j}^d \Big(T_{j l}({\mathbf x})+T_{l j}({\mathbf x}) \Big)\end{align} }
Note that the diffusion matrix is symmetric, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal B}_{jk}({\mathbf x}) = {\mathcal B}_{kj}({\mathbf x})} and vanishes as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sim 1/N} in the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\to\infty} .
The noise arising through demographic changes and mutations is uncorrelated in time and hence the Itô calculus can be applied to derive a Langevin equation
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot x_k = {\mathcal A}_k({\mathbf x}) + \sum_{j=1}^{d-1} {{\mathcal C}_{kj}({\mathbf x})} \xi_j(t) }
where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_j(t)} represent uncorrelated Gaussian white noise with unit variance, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \xi_k(t) \xi_j(t^\prime) \rangle = \delta_{kj} \delta(t-t^\prime)} . The matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {{\mathcal C}({\mathbf x})}} is defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal C}^T({\mathbf x}) {\mathcal C}({\mathbf x}) = {\mathcal B}({\mathbf x})} and its off-diagonal elements are responsible for correlations in the noise of different strategic types. In the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\to\infty} the matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal C}({\mathbf x})} vanishes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sim 1/\sqrt{N}} and we recover a deterministic replicator mutator equation.
References
- Traulsen, A., Claussen, J. C. & Hauert, C. (2012) Stochastic differential equations for evolutionary dynamics with demographic noise and mutations. Phys. Rev. E in print.
- Traulsen, A., Claussen, J. C. & Hauert, C. (2006) Coevolutionary dynamics in large, but finite populations. Phys. Rev. E 74 011901 doi: 10.1103/PhysRevE.74.011901.
- Traulsen, A., Claussen, J. C. & Hauert, C. (2005) Coevolutionary Dynamics: From Finite to Infinite Populations. Phys. Rev. Lett. 95 238701 doi: 10.1103/PhysRevLett.95.238701.