Evolutionary Games and Population Dynamics
The emergence and abundance of cooperation in nature poses a tenacious and challenging puzzle to evolutionary biology. Cooperative behavior seems to contradict Darwinian evolution because altruistic individuals increase the fitness of other members of the population at a cost to themselves. Thus, in the absence of supporting mechanisms, cooperation should decrease and vanish, as predicted by classical models for cooperation in evolutionary game theory, such as the prisoner's dilemma and public goods games.
In typical public goods games individuals interact in groups of size \(N\). Cooperators contribute to a common pool at some cost \(c\) while defectors shirk their contributions. The total amount in the common pool is multiplied by a factor \(r\) and evenly distributed among all participants irrespective of their contributions. Defectors attempt to free ride on the contributions of others and because they avoid the costly contributions they are always better off than cooperators. However, if everyone reasons that way the public good is forfeit, yet everyone would prefer the outcome where everyone contributes and earns a payoff of \((r-1)c\). This marks the conflict of interest between the individual and the group that characterizes all social dilemmas.
Traditional approaches to the problem of cooperation based on the replicator dynamics assume constant (infinite) population sizes and thus neglect the ecology of the interacting individuals. Here we incorporate ecological dynamics into evolutionary games and reveal a new mechanism for maintaining cooperation whenever the population density depends on the average population payoff. Defection decreases the population density, due to small payoffs, resulting in smaller interaction group sizes in which cooperation may be favoured. This feedback between ecological dynamics and game dynamics generates fascinating and rich dynamical behavior. Such Ecological Public Goods Games represent natural extension of replicator dynamics to populations of varying densities.
Bifurcations in well-mixed populations
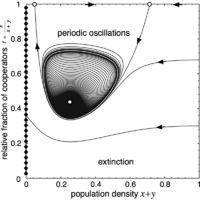
In infinite populations where individuals randomly interact in public goods games, cooperators are doomed and readily disappear. In contrast, varying population densities can lead to stable coexistence of cooperators and defectors in public goods games. When increasing the efficiency of the public good the system undergoes a series of bifurcations and the dynamics ranges from extinction, to periodic oscillations and finally stable co-existence.
Pattern formation in spatial populations

Spatial 'reaction-diffusion' dynamics promotes cooperation based on different types of pattern formation processes. Individuals can migrate (diffuse) in order to populate new territories. Slow diffusion of cooperators fosters aggregation in highly productive patches (activation), whereas fast diffusion enables defectors to readily locate and exploit these patches (inhibition). These antagonistic forces promote co-existence of cooperators and defectors in static or dynamic patterns, including spatial chaos of ever changing configurations.
Ecological Public Goods
The replicator equation describes the change in frequencies of cooperators over evolutionary time. The Moran process does the same for finite populations. In either case, the motivating assumption is that the population is in ecological equilibrium and has reached its carrying capacity. This also assumes that the population dynamics can be neglected over evolutionary time. While this is reasonable in many circumstances it can be problematic if, for example, the ecological dynamics exhibits stable limit cycles. Clearly this may have an impact on the evolutionary dynamics as the success of mutants may depend on the timing of their occurrence.
However, a more serious concern arises from the fact that groups of cooperators have a higher fitness than groups of defectors. In an ecological context higher fitness usually translates into larger population sizes or densities. Only in special cases would, for example, an increase in the reproductive rate leave the carrying capacity unaffected because the effect is exactly cancelled by an equal increase competition. Nevertheless, this is exactly the underlying assumptions of the replicator dynamics or the Moran process: the population size remains unaffected by the population composition.
Ecological Public Goods games take this into account by considering the frequency of cooperators \(u\) and of defectors \(v\) with \(u+v\leq1\). The (normalized) population density \(u+v\) affect the public goods interactions in that only smaller groups may successfully form at low population densities. Interaction groups of up to size \(N\) are randomly sampled where each trial adds a cooperator with probability \(u\), a defector with \(v\) and fails to add another member with probability \(1-u-v\). Hence the expected interaction group size is \(\bar S=(u+v)N\) and varies with population density.
Payoffs of cooperators and defectors
In order to determine the average payoff for cooperators \(f_C\) and defectors \(f_D\) in a population with a normalized density of cooperators, \(u\), and of defectors, \(v\), with \(u+v\leq1\), it is convenient to introduce a new quantity \(w=1-u-v\) which represents reproductive opportunities. If \(w\) approaches one, competition for limited resources, such as space or food, becomes fierce and offspring may not reach adulthood but if \(w\) is small, population densities are low and reproductive opportunities abound. However, at low densities, individuals may no longer be able to find interaction partners. If the public goods group consist of only a single individual no payoffs are awarded as no social interaction occurs. In ecology such density dependence is known as the Allee effect.
For a given player willing to join the public goods interaction, the probability to find itself in a group of \(S>1\) players is given by \[{N-1 \choose S-1}(1-w)^{S-1}w^{N-S}.\] The probability that there are \(m\) cooperators among the \(S-1\) co-players is \[\left({\frac u{u+v}}\right)^m \left({\frac v{u+v}}\right)^{S-1-m}{S-1 \choose m}.\] In that case the payoff for a defector is \(r m c/S\) where \(r\) is the multiplication factor of the total contributions to the public good and \(c\) the costs of contributing. Hence the expected payoff for a defector in a group of \(S\) players (\(S=2,...,N\)) is \begin{align*} {\frac{r c}S \sum _{m=0}^{S-1} m }\left({\frac u{u+v}}\right)^m \left({\frac v{u+v}}\right)^{S-1-m}{S-1 \choose m} = \frac{r c}S(S-1)\frac u{u+v}. \end{align*} Thus, \begin{align*} f_D =& r c\frac u{1-w}\sum _{S=1}^{N}{N-1 \choose S-1}(1-w)^{S-1}w^{N-S}\left(1-\frac{1}{S}\right)\\ =& r c\frac u{1-w}\left[1-\sum _{S=1}^{N}{N-1 \choose S-1}(1-w)^{S-1}w^{N-S}\frac1S\right] \end{align*} and using \({N-1 \choose S-1}={N \choose S}\frac{S}{N}\) leads to \begin{align*} f_D=& r\frac u{1-w}\left(1-\frac{1-w^N}{N(1-w)}\right)c. \end{align*} In a group with \(S-1\) co-players playing the public goods game, switching from cooperation to defection yields \((1-r/S)c\). Hence, \begin{align*} f_D-f_C=& \sum _{S=2}^N\left(1-{\frac rS}\right){N-1 \choose S-1}(1-w)^{S-1}w^{N-S}c. \end{align*} Using the same arguments as before, we obtain \begin{align*} f_D-f_C=& \left(\!1+(r-1)w^{N-1}-\frac rN{\frac{1-w^N}{1-w}}\right)c =: F(w). \end{align*} The payoff derivation follows [1]. Note that the payoff difference between cooperators and defectors only depends on the \(w\), that is on the population density. The sign of \(F(w)\) determines whether it pays to switch from cooperation to defection or vice versa. It turns out that for \(r<2\) it never pays to switch to cooperation but for \(r>2\), \(F(w)\) has a unique root for \(w\in(0,1)\) and hence a critical population density exists below which it pays to switch to cooperation. This occurs whenever the average interaction group size \(\bar S\) drops below the multiplication factor \(r\). Defectors still outperform cooperators in any mixed group but on average, cooperators are better off (such situations are known as Simpson's paradox). However, in that case, defectors would be even better off by switching to cooperation because each dollar invested in the common pool has a positive return for the investor.
References
Ecological Public Goods
- Wakano, J. Y. & Hauert, C. (2011) Pattern formation and chaos in spatial ecological public goods games, J. theor. Biol. 268 30-38 doi: 10.1016/j.jtbi.2010.09.036.
- Wakano, J. Y., Nowak, M. A. & Hauert, C. (2009) Spatial Dynamics of Ecological Public Goods, Proc. Natl. Acad. Sci. USA 106 7910-7914 doi: 10.1073/pnas.0812644106.
- Hauert, C., Wakano, J. Y. & Doebeli, M. (2008) Ecological Public Goods Games: cooperation and bifurcation, Theor. Pop. Biol. 73, 257-263 doi:10.1016/j.tpb.2007.11.007.
- Hauert, C., Holmes, M. & Doebeli, M. (2006) Evolutionary games and population dynamics: maintenance of cooperation in public goods games, Proc. R. Soc. Lond. B 273, 2565-2570 doi: 10.1098/rspb.2006.3600; Addendum: Proc. R. Soc. Lond B 273, 3131-3132 doi: 10.1098/rspb.2006.3717.
Supporting articles
- ↑ Hauert, Ch., De Monte, S., Hofbauer, J. & Sigmund, K. (2002) Replicator Dynamics in Optional Public Goods Games, J. theor. Biol. 218, 187-194 doi: 10.1006/jtbi.2002.3067.
