2×2 Games/Spatial populations: Difference between revisions
No edit summary |
mNo edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | {{InCharge|author1=Christoph Hauert}}__NOTOC__ | ||
In spatially structured populations the performance of an individual is determined through interactions within a limited local neighborhood rather than through interactions with randomly selected members of the population as in the case of well-mixed populations. In particular, for the Prisoner's Dilemma it is well-known that including spatial extensions enables cooperators to thrive by forming clusters and thereby reducing exploitation through defectors. Whereas in well-mixed populations cooperators invariably dwindle and disappear. Quite naturally, the inclusion of spatial dimensions (or any type of population structure) can have pronounced effects on the evolutionary dynamics of other | In spatially structured populations the performance of an individual is determined through interactions within a limited local neighborhood rather than through interactions with randomly selected members of the population as in the case of well-mixed populations. In particular, for the Prisoner's Dilemma it is well-known that including spatial extensions enables cooperators to thrive by forming clusters and thereby reducing exploitation through defectors. Whereas in well-mixed populations cooperators invariably dwindle and disappear. Quite naturally, the inclusion of spatial dimensions (or any type of population structure) can have pronounced effects on the evolutionary dynamics of other \(2\times2\) games, too. | ||
[[Image:Spatial 2x2 Games (difference).png|thumb|right|305px|Effects of space in \(2\times2\) Games: Differences in the equilibrium level of \(A\) types in spatial settings as compared to well-mixed populations. In blue areas the frequency of \(A\)'s is increased but decreased in red areas. The saturation of the colors indicates the strength of the effect.]] | |||
[[Image:Spatial 2x2 Games.png|thumb|left|305px|Spatial \(2\times2\) Games: equilibrium levels of \(A\) and \(B\) types in the \(S,T\)-plane (with \(R=1, P=0\) ). The color code indicates the equilibrium frequency of type \(A\) ranging from low, red to intermediate, green and high, blue.]] | |||
This interactive tutorial encourages the exploration of the rich and fascinating dynamics of such simple models. In addition there are several sample scenarios described in more detail which emphasize the most important findings of this line of research. | |||
For symmetrical initial configurations on regular lattices with deterministic update rules - such as imitating the strategy of the best performing neighbour - the initial symmetry is preserved and the lattice resembles a dynamically changing persian carpet or an [[Evolutionary Kaleidoscopes|evolutionary kaleidoscope]]. | |||
{{-}} | {{-}} | ||
== Dynamical regimes == | == Dynamical regimes == | ||
A simple analysis of | A simple analysis of \(2\times2\) games in well-mixed populations (or in the mean-field approximation) reveals four regimes with different dynamics. The spatial extension or more generally the population structure leads to several important modifications but essentially the four dynamical domains still exist. | ||
{{Legend:StrategiesCD}} | {{Legend:StrategiesCD}} | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:Spatial 2x2 Game - Dominance A.png|left|200px]] | [[Image:Spatial 2x2 Game - Dominance A.png|left|200px|link=EvoLudoLab: Spatial 2x2 Game - Dominance A]] | ||
==== [[ | ==== [[EvoLudoLab: Spatial 2x2 Game - Dominance A|Type A dominates]]==== | ||
For | For \(T<1\) and \(S>0\) a well-mixed population eventually relaxes into a homogenous state of cooperators regardless of the initial configuration. In spatially extended systems this is generally equally true. However, for small \(S\) it becomes increasingly unlikely that an isolated type \(A\) individual is able to expand - obviously this depends on the individuals' update rule. When sparse, small clusters of \(A\)'s can act as seeds for their future success. | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:Spatial 2x2 Game - Dominance B.png|left|200px]] | [[Image:Spatial 2x2 Game - Dominance B.png|left|200px|link=EvoLudoLab: Spatial 2x2 Game - Dominance B]] | ||
==== [[ | ==== [[EvoLudoLab: Spatial 2x2 Game - Dominance B|Type B dominates]]==== | ||
For | For \(T>1\) and \(S<0\) type \(A\) individuals go extinct and \(B\)'s reign in well-mixed populations. This is generally equally true in spatially extended systems. However, some exceptions apply for small \(T\) and large \(S\). | ||
This scenario is particularly important because it includes the prisoner's dilemma, where | This scenario is particularly important because it includes the prisoner's dilemma, where \(A\) denotes cooperation and \(B\) defection. With a deterministic update rule for the individuals, clusters of cooperators can survive roughly as long as \(T<S+5/3\) holds. Adding noise to either the update rule of the players or the population tends to further decrease this area. Outside this small parameter region the system quickly relaxes into homogenous states with all defectors (for further details see the tutorial on [[Cooperation in structured populations]]). | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:Spatial 2x2 Game - Coexistence.png|left|200px]] | [[Image:Spatial 2x2 Game - Coexistence.png|left|200px|link=EvoLudoLab: Spatial 2x2 Game - Coexistence]] | ||
==== [[ | ==== [[EvoLudoLab: Spatial 2x2 Game - Coexistence|Coexistence]]==== | ||
In well-mixed populations co-existence requires that | In well-mixed populations co-existence requires that \(T>1\) and \(S>0\). The equilibrium frequency of cooperators is given by \(x_3=S/(S+T-1)\) with \(R=1, P=0\). In spatially extended systems almost independently of the initial configuration \(A\) and \(B\) types coexist in equilibrium but interestingly, generally spatial extensions tends to favour \(B\)'s. | ||
The most prominent representative of this category is the [[Snowdrift Game]], [[Hawk-Dove Game|Hawk-Dove]] or [[Chicken|Chicken game]] (all are mathematically equivalent and require additionally that | The most prominent representative of this category is the [[Snowdrift Game]], [[Hawk-Dove Game|Hawk-Dove]] or [[Chicken|Chicken game]] (all are mathematically equivalent and require additionally that \(S<1\)). Recently, the Snowdrift Game attracted increasing attention as a biologically viable alternative to the Prisoner's Dilemma for modeling cooperative interactions. Most importantly, the detrimental effects of space on the equilibrium levels of cooperation in the Snowdrift game have cautioned against the general believe that spatial structure is necessarily beneficial for cooperation (for further details see the tutorial on [[Cooperation in structured populations]]). | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:Spatial 2x2 Game - Bistability.png|left|200px]] | [[Image:Spatial 2x2 Game - Bistability.png|left|200px|link=EvoLudoLab: Spatial 2x2 Game - Bistability]] | ||
==== [[ | ==== [[EvoLudoLab: Spatial 2x2 Game - Bistability|Bistability]]==== | ||
Well-mixed populations with | Well-mixed populations with \(T<1\) and \(S<0\) are bi-stable, i.e. depending on the initial configuration the system approaches either a homogenous state of \(A\) or \(B\). In this parameter range spatial extension has the most pronounced effect on the long term fate of either strategy. The parameter values \(S, T\) determine the stability i.e. average lifetime of certain local configurations. The probability for their creation at initialization time sensitively depends on the initial fraction of cooperators. | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
[[Category: | [[Category:2×2 games]][[Category:Tutorial]] | ||
[[Category: | |||
Latest revision as of 15:16, 23 August 2016
In spatially structured populations the performance of an individual is determined through interactions within a limited local neighborhood rather than through interactions with randomly selected members of the population as in the case of well-mixed populations. In particular, for the Prisoner's Dilemma it is well-known that including spatial extensions enables cooperators to thrive by forming clusters and thereby reducing exploitation through defectors. Whereas in well-mixed populations cooperators invariably dwindle and disappear. Quite naturally, the inclusion of spatial dimensions (or any type of population structure) can have pronounced effects on the evolutionary dynamics of other \(2\times2\) games, too.
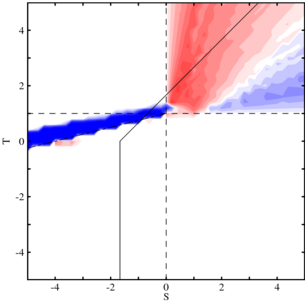

This interactive tutorial encourages the exploration of the rich and fascinating dynamics of such simple models. In addition there are several sample scenarios described in more detail which emphasize the most important findings of this line of research.
For symmetrical initial configurations on regular lattices with deterministic update rules - such as imitating the strategy of the best performing neighbour - the initial symmetry is preserved and the lattice resembles a dynamically changing persian carpet or an evolutionary kaleidoscope.
Dynamical regimes
A simple analysis of \(2\times2\) games in well-mixed populations (or in the mean-field approximation) reveals four regimes with different dynamics. The spatial extension or more generally the population structure leads to several important modifications but essentially the four dynamical domains still exist.
| Color code: | Cooperators | Defectors |
|---|---|---|
| New cooperator | New defector |

Type A dominates
For \(T<1\) and \(S>0\) a well-mixed population eventually relaxes into a homogenous state of cooperators regardless of the initial configuration. In spatially extended systems this is generally equally true. However, for small \(S\) it becomes increasingly unlikely that an isolated type \(A\) individual is able to expand - obviously this depends on the individuals' update rule. When sparse, small clusters of \(A\)'s can act as seeds for their future success.

Type B dominates
For \(T>1\) and \(S<0\) type \(A\) individuals go extinct and \(B\)'s reign in well-mixed populations. This is generally equally true in spatially extended systems. However, some exceptions apply for small \(T\) and large \(S\).
This scenario is particularly important because it includes the prisoner's dilemma, where \(A\) denotes cooperation and \(B\) defection. With a deterministic update rule for the individuals, clusters of cooperators can survive roughly as long as \(T<S+5/3\) holds. Adding noise to either the update rule of the players or the population tends to further decrease this area. Outside this small parameter region the system quickly relaxes into homogenous states with all defectors (for further details see the tutorial on Cooperation in structured populations).
Coexistence
In well-mixed populations co-existence requires that \(T>1\) and \(S>0\). The equilibrium frequency of cooperators is given by \(x_3=S/(S+T-1)\) with \(R=1, P=0\). In spatially extended systems almost independently of the initial configuration \(A\) and \(B\) types coexist in equilibrium but interestingly, generally spatial extensions tends to favour \(B\)'s.
The most prominent representative of this category is the Snowdrift Game, Hawk-Dove or Chicken game (all are mathematically equivalent and require additionally that \(S<1\)). Recently, the Snowdrift Game attracted increasing attention as a biologically viable alternative to the Prisoner's Dilemma for modeling cooperative interactions. Most importantly, the detrimental effects of space on the equilibrium levels of cooperation in the Snowdrift game have cautioned against the general believe that spatial structure is necessarily beneficial for cooperation (for further details see the tutorial on Cooperation in structured populations).

Bistability
Well-mixed populations with \(T<1\) and \(S<0\) are bi-stable, i.e. depending on the initial configuration the system approaches either a homogenous state of \(A\) or \(B\). In this parameter range spatial extension has the most pronounced effect on the long term fate of either strategy. The parameter values \(S, T\) determine the stability i.e. average lifetime of certain local configurations. The probability for their creation at initialization time sensitively depends on the initial fraction of cooperators.
