2×2 Games/Well-mixed populations: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{InCharge|author1=Christoph Hauert}} | |||
__NOTOC__ | __NOTOC__ | ||
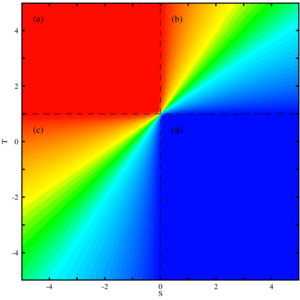
[[Image:Well-mixed 2x2 Games.png|thumb|300px|Four basic evolutionary scenarios of 2×2 Games in the | |||
In well-mixed populations the equilibrium fractions of cooperators and defectors are easily calculated using the replicator equation. If | |||
\begin{align} | |||
\qquad\dot x = \frac{dx}{dt} = x(1-x)(P_A-P_B) | |||
\end{align} | |||
where | |||
\begin{align} | |||
\qquad x_3 = \frac{P-S}{R-S-T+P}. | |||
\end{align} | |||
The replicator equation allows to shift and normalize the payoffs without affecting the dynamics because the performance of cooperators and defectors only depends on the relative payoffs, i.e. on payoff differences. For this reason we can set \(R=1\) and \(P=0\) without loss of generality. Note that the equilibrium | |||
{{-}} | |||
== Basic evolutionary scenarios == | == Basic evolutionary scenarios == | ||
All of the following examples and suggestions are meant as inspirations for further experimenting with the '' | All of the following examples and suggestions are meant as inspirations for further experimenting with the ''EvoLudo'' simulator. Each of following examples starts a lab that demonstrates the particular dynamical scenario. By modifying the [[Parameters|parameters]] the dynamics can be further explored. | ||
{{Legend:PlainAB|a=Type A|b=Type B}} | {{Legend:PlainAB|a=Type A|b=Type B}} | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:2x2 Game - Dominance A.svg|left|200px]] | [[Image:2x2 Game - Dominance A.svg|left|200px|link=EvoLudoLab: 2x2 Game - Dominance A]] | ||
==== [[ | ==== [[EvoLudoLab: 2x2 Game - Dominance A|Type A dominates]]==== | ||
For | For \(T<1\) and \(S>0\) the only stable equilibrium is \(x_2=1\) (\(x_1=0\) is unstable and \(x_3\) does not exist). Thus, regardless of the initial configuration of the population type \(A\) will increase and eventually reach fixation. | ||
If | If \(A\) indicates cooperation and \(B\) defection, then cooperation dominates defection. In biology, this situation refers to by-product mutualism, where cooperative behavior establishes as a by-product of some other activity. For example, the of stotting gazelles is cooperative behavior because it warns their fellows from approaching predators but at the same time it startles predators and displays the individuals strength, which might persuade the predator to go after another individual. The relative costs and benefits of these two aspects of stotting behavior determine whether warning other gazelles occurs only as a by-product. | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:2x2 Game - Dominance B.svg|left|200px]] | [[Image:2x2 Game - Dominance B.svg|left|200px|link=EvoLudoLab: 2x2 Game - Dominance B]] | ||
==== [[ | ==== [[EvoLudoLab: 2x2 Game - Dominance B|Type B dominates]]==== | ||
Conversely, for | Conversely, for \(T>1\) and \(S<0\) the only stable equilibrium is \(x_1=0\) (\(x_2=1\) is unstable and \(x_3\) does not exist). Thus, type \(A\) players eventually disappear irrespective of the initial configuration of the population. | ||
If | If \(A\) indicates cooperation and \(B\) defection, then defection dominates cooperation. In biology, this situation is represented by the famous [[Prisoner's Dilemma]] (for further details see the tutorial on [[Cooperation in structured populations]]). | ||
{{-}} | {{-}} | ||
</div> | </div> | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:2x2 Game - Coexistence.svg|left|200px]] | [[Image:2x2 Game - Coexistence.svg|left|200px|link=EvoLudoLab: 2x2 Game - Coexistence]] | ||
==== [[ | ==== [[EvoLudoLab: 2x2 Game - Coexistence|Coexistence]]==== | ||
For | For \(T>1\) and \(S>0\) both trivial equilibria \(x_1, x_2\) are unstable and the equilibrium \(x_3\) must exist and must be stable. In that case, type \(A\) and \(B\) individuals can co-exist. | ||
This situation corresponds to the [[Snowdrift game]], [[Chicken]] or [[Hawk-Dove game]] used to model cooperation and competition in biology (for further details see the tutorial on [[Cooperation in structured populations]]). | This situation corresponds to the [[Snowdrift game]], [[Chicken]] or [[Hawk-Dove game]] used to model cooperation and competition in biology (for further details see the tutorial on [[Cooperation in structured populations]]). | ||
| Line 46: | Line 47: | ||
<div class="lab_description 2x2"> | <div class="lab_description 2x2"> | ||
[[Image:2x2 Game - Bistability.svg|left|200px]] | [[Image:2x2 Game - Bistability.svg|left|200px|link=EvoLudoLab: 2x2 Game - Bistability]] | ||
==== [[ | ==== [[EvoLudoLab: 2x2 Game - Bistability|Bistability]]==== | ||
Finally, for | Finally, for \(T<1\) and \(S<0\) both trivial equilibria are stable with an unstable equilibrium \(x_3\) in the interior. Depending on the initial configuration of the population either cooperators or defectors will increase and reach fixation. The position of \(x_3\) determines the basin of attraction of the evolutionary end states of all cooperation or all defection. If the initial fraction of cooperators exceeds \(x_3\) then the \(A\) types prevail but vanish otherwise. | ||
This situation represent a coordination game often referred to as a [[Staghunt game]]. | This situation represent a coordination game often referred to as a [[Staghunt game]]. | ||
| Line 55: | Line 56: | ||
[[Category:Tutorial]] | [[Category:Tutorial]] | ||
Latest revision as of 15:20, 13 October 2023
In well-mixed populations the equilibrium fractions of cooperators and defectors are easily calculated using the replicator equation. If
The replicator equation allows to shift and normalize the payoffs without affecting the dynamics because the performance of cooperators and defectors only depends on the relative payoffs, i.e. on payoff differences. For this reason we can set
Basic evolutionary scenarios
All of the following examples and suggestions are meant as inspirations for further experimenting with the EvoLudo simulator. Each of following examples starts a lab that demonstrates the particular dynamical scenario. By modifying the parameters the dynamics can be further explored.
| Color code: | Type A | Type B |
|---|

Type A dominates
For
If

Type B dominates
Conversely, for
If

Coexistence
For
This situation corresponds to the Snowdrift game, Chicken or Hawk-Dove game used to model cooperation and competition in biology (for further details see the tutorial on Cooperation in structured populations).
Bistability
Finally, for
This situation represent a coordination game often referred to as a Staghunt game.
