Cooperation in well-mixed populations

The evolution of cooperation under Darwinian selection challenges scientists across behavioral disciplines - from evolutionary biology to social sciences and economics. Over the last decades the Prisoner's Dilemma as the leading mathematical metaphor to investigate cooperative interactions using Game Theory. Interestingly, the tremendous success of the Prisoner's Dilemma in theoretical studies is met by a surprising lack of specific empirical evidence. Therefore, in many situations interactions might be better captured by the Snowdrift game, which represents a biologically interesting alternative to model cooperative interactions under less stringent conditions. The Snowdrift Game is also known as the Hawk-Dove Game or Chicken Game.

This tutorial contrasts the evolutionary outcomes for the Prisoner's Dilemma and the Snowdrift Game. It is divided into to parts: the first part considers unstructured (or well-mixed) populations where individuals randomly interact with other members of the population. These results form the basis for the second part of the tutorial on spatially structured populations with limited local interactions and highlights the different effects of spatial extension on the evolutionary dynamics in the two games.

This tutorial represents the prelude to the results reported in a research article with Michael DoebeliinNature (2004) 428 643-646. For further details please refer to Cooperation in structured populations.

Dynamical scenarios

Pure strategies

In well-mixed populations the dynamics of the Prisoner's Dilemma and Snowdrift or Hawk-Dove game can be fully analyzed. Besides, in well-mixed populations there is no distinction between pure or mixed strategies. These results provide the basis for the discussion of effects of spatial structuring in populations on the fate of cooperative behavior.

Color code:	Cooperators	Defectors

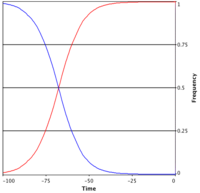
Prisoner's Dilemma: extinction of cooperators

The Prisoner's Dilemma is characterized by the payoff ranking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>R>P>S} , which means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=0} is stable, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=1} unstable and hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3} does not lie in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,1)} . Therefore, regardless of the initial configuration of the population cooperators are bound to go extinct. Consequentially everybody in the population ends up with the payoff Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} instead of the preferrable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} for mutual cooperation - and hence the dilemma.

The sample simulation shows the time evolution of the fraction of cooperators in a well-mixed population playing the Prisoner's Dilemma when starting with 99% cooperators.

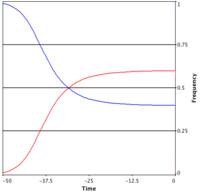
Snowdrift Game: co-existence of cooperators and defectors

For the Snowdrift and Hawk-Dove game the characteristic payoff ranking is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>R>S>P} . From the above calculation follows that now both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=1} are unstable and hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3} exists and is stable. Consequentially, a stable mixture of cooperators and defectors evolves. Note that the average population payoff in equilibrium is smaller than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} - just as in the Prisoner's Dilemma. Thus, the paradox of cooperation is also apparent in the Snowdrift or Hawk-Dove games.

The sample simulation shows the time evolution of the fraction of cooperators in a well-mixed population playing the Snowdrift or Hawk-Dove game. Since the sample simulations consider finite populations, small fluctuations around the equilibrium occur.

Mixed strategies

The results for well-mixed populations do not depend on whether they refer to individuals with pure or mixed strategies. However, the interpretation of the underlying mechanisms is quite different and, in particular, the continuous strategy space of mixed strategies requires the introduction of mutations.

Strategies:	Maximum	Minimum	Mean

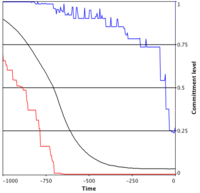
Prisoner's Dilemma: gradual demise of cooperation

In the Prisoner's Dilemma mutants with lower probabilities to cooperate are better off which leads to a continuous decrease of the readiness to cooperate in the population until cooperative behavior vanishes.

The sample simulation shows the time evolution of the readiness to cooperate in a well-mixed population playing the Prisoner's Dilemma when starting with a mean initial propensity to cooperate of 99% in a population of 10'000 individuals.

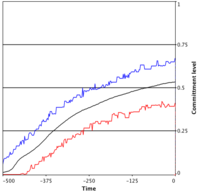
Snowdrift Game: intermediate readiness to cooperate

In the Snowdrift or Hawk-Dove game the success of mutant strategies depends on the current state/composition of the population. The mean readiness to cooperate eventually approaches an intermediate value as specified by the fixed point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3} .

The sample simulation shows the time evolution of the readiness to cooperate in a well-mixed population playing the Snowdrift or Hawk-Dove game when starting with an initial mean propensity to cooperate of 1% in a population of 10'000 individuals.

Notes for mixed strategy simulations

In individual based simulations, mutations lead to some variance in the strategies present in the population and therefore the applets plot not only the mean propensity to cooperate but also the minimum and maximum values. Besides, in biologically motivated models it is reasonable to assume that mutations add only minor changes to the parental strategy. Therefore mutants are assigned a new strategy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=p+s} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} is the parental strategy and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} is a Gaussian distributed random variable with a small standard deviation. For small standard deviations the difference in payoffs for mutants and residents becomes very small. This can result in an enormous slowing down of the simulations because the reproductive success is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_q-P_p} . To avoid this we set the reproductive success proportional to \begin{align} \qquad \frac{1}{1+\exp\left(\frac{P_q-P_p}{k}\right)}, \end{align} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} denotes a noise term. With this rule, small differences in payoffs are amplified for small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and in addition it introduces an interesting form of errors since worse performing individuals may still manage to reproduce with a small probability - which is certainly a reasonable assumption in an imperfect world. Strictly speaking this update rule no longer corresponds to the replicator equation but it still reproduces the essential results even quantitatively. The update rule of the players is one of the many parameters that can be changed in the EvoLudo simulator and you are encouraged to compare the two approaches.

Dynamics of pure strategies

In well-mixed populations the equilibrium fractions of cooperators and defectors are easily calculated using the replicator equation: \begin{align} \qquad\frac{dx_i}{dt}= x_i (P_i - \bar P), \end{align} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_i} denotes the frequency, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_i} the payoff (fitness) of strategy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar P} the average population payoff. The replicator equation simply states that the success of a strategy depends on its relative performance in the population. Therefore, strategies with a higher than average payoff will spread. In a population with a fraction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} cooperators and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=1-x} defectors the replicator equation reduces to \begin{align} \qquad\frac{dx}{dt} = x(1-x)(P_c-P_d), \end{align} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_c} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_d} denote the average payoffs of cooperators and defectors, respectively. The above equation has three equilibria: two trivial ones with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=1} as well as a non-trivial one for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_c=P_d} which leads to \begin{align} \qquad x R+(1-x) S = x T+(1-x)P \end{align} and \begin{align} \qquad x_3 = (S-P)/(T+S-R-P). \end{align}

The stability of all three equilibrium points is easily obtained by checking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx/dt} near the equilibium points: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=0} is stable if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P > S} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=1} stable if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R > T} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3} is stable if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S > P} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T > R} , i.e. whenever both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2} are unstable.

Instead of referring to the fraction of cooperators, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} may equally refer to the propensity of cooperation in a continuous strategy space (see next section and examples above). This equivalent interpretation leaves the above calculations and conclusions unaffected but it does affect the individual based simulations. In particular, we need to introduce mutations. The replicator equation then determines the fate of a rare mutant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} when competing against the resident Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . If the mutation is favorable the mutant will spread and usually displace the resident.

Dynamics of mixed strategies

For the pure strategies, to cooperate or to defect, the above analysis has shown that the replicator dynamics up to three equilibria: The homogenous states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=1} with all defectors or all cooperators, respectively, as well as potentially a mixed equilibrium Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3=(S-P)/(T+S-R-P)} where cooperators and defectors may co-exist provided that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3} lies in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,1)} .

Essentially the same results hold for well-mixed populations adopting mixed strategies, i.e. if every individual cooperates with a certain probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} . This propensity to cooperate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} evolves towards one of the fixed points derived for pure strategies. To illustrate this, consider a homogenous population where all individuals cooperate with probability $p$ . The fate of a rare mutant $q$ is then given by \begin{align} \qquad \frac{dm}{dt} = m(P_q-\bar P), \end{align} where $m$ denotes the frequency of the mutant and ${\bar {P}}$ the average population payoff. As long as the mutant strategy is rare this can be approximated by \begin{align} \qquad \frac{dm}{dt} = m(P_q-P_p), \end{align} which means the mutant can invade whenever $P_{q}-P_{p}>0$ . Again for small $m$ we obtain \begin{align} \qquad P_q =&\ p q R + p(1-q)S+(1-p)q\, T+(1-p)(1-q) P\\ P_p =&\ p q R + p(1-q)T+(1-p)q\, S + (1-p)(1-q) P, \end{align} respectively. Thus, $q$ successfully invades whenever \begin{align} \qquad (q - p)[p(R-T)+(1-p)(S-P)] > 0 \end{align} holds. This result can now be applied to the Prisoner's Dilemma and Snowdrift or Hawk-Dove games. The Prisoner's Dilemma is characterized by $T>R>P>S$ and therefore the expression in square brackets is always negative. Consequentially, any mutant with $q<p$ can invade and take over the population (the latter can be derived from the first equation which is not restricted to rare mutants). Thus, in the long run, the propensity to cooperate converges to $x_{1}=0$ - just as in the pure strategy case.

The argument for the Snowdrift or Hawk-Dove game is slighlty more complicated. Because of the payoff ranking $T>R>S>P$ the expression in square brackets can be both positive or negative, depending on the value of $p$ . It switches sign for \begin{align} \qquad p=(S-P)/(T-R+S-P)=x_3. \end{align}

For simplicity let us consider only mutants with arbitrarily small deviations from the resident strategy $p$ . It follows that for $p<x_{3}$ , a mutant with a slightly higher $q$ can invade but if $p>x_{3}$ only mutants with slightly lower $q$ can invade. Thus, eventually the propensity to cooperate in the population converges to $x_{3}$ - again as in the case of pure strategies.

Note that the above argument is easily generalized to random, arbitrarily large mutations but then one can no longer assume homogenous resident populations. Rather, the resident population may consist of a mixture of two strategies $p,p'$ , with $p<x_{3}<p'$ . But then the mutant $q$ either satisfies the conditions for invasion for $p$ and $p'$ or for neither of them.